Revizia anterioară Revizia următoare
Solutii Happy Coding 3
Concursurile Happy Coding par sa fie singurele care nu au avut parte de descrieri ale solutiilor problemelor propuse.. Desi cu intarziere, intentionez sa remediez aceasta situatie. Aceasta pagina este "under construction" momentan.
O parte din problemele date in cadrul acestui concurs (cele propuse de Mugurel Ionut Andreica) au fost folosite pentru a selecta echipele care au reprezentat Universitatea Politehnica Bucuresti la etapa regionala sud-est europeana a concursului ACM ICPC, in anul 2006.
AVD
Cea mai simpla solutie consta in generarea tuturor submultimilor de muchii pe care le eliminam. Ce ramane este o reuniune de componente conexe, care defineste fiecare cate o partitie. Dintre toate cele 2N-1 partitii generate, le pastram pe cele unice si impartim acest numar la numarul total de partitii (care poate fi generat si el prin backtracking sau folosind programare dinamica).
O solutie mai laborioasa consta in generarea fiecarei partitii (putin peste 100, pt N=13) si, pentru fiecare astfel de partitie (care are, sa presupunem K elemente), calcularea urmatoarelor valori: ok[i][j][S] = 1 sau 0 , reprezentand daca e posibil sau nu sa se "acopere" elementele partitiei corespunzatoare starii S ($S$ e un numar pe K biti), folosind nodurile din subarborele lui i si ramanand j noduri, inclusiv nodul i, intr-o componenta conexa pe care nu o "potrivim" peste vreun element al partitiei (si care poate fi eventual extinsa ulterior de catre un stramos al lui i); o valoare j=0 indica ca au fost folosite toate nodurile din subarborele lui i, inclusiv i, pentru a genera componente conexe care se "potrivesc" peste elemente ale partitiei. Aceste valori se calculeaza folosind programare dinamica de tip rucsac pe arbore, in functie de valorile calculate pentru fii (valori de tipul ok[fiu][j'][S'], cu j' < j si S' inclus in S). Daca ok[ 1 ][ 0 ][2K-1] are valoarea 1, atunci se poate genera o impartire in componente conexe a arborelui, ce corespunde partitiei respective.
CT
Se fixeaza radacina arborelui intr-un nod (sa zicem nodul 1). Pentru fiecare din cele K perechi de orase se calculeaza LCA-ul (lowest common ancestor = cel mai apropiat stramos comun). Se poate folosi orice metoda eficienta de determinarea a LCA-ului: de exemplu, pentru fiecare nod i se pot memora O(logN) valori, stramos[i][j], reprezentand stramosul aflat cu 2j nivele mai sus in arbore (cu j incepand de la 0), iar cu aceste valori, LCA-ul a oricare 2 noduri se poate determina in timp O(logN). Se sorteaza apoi LCA-urile tuturor perechilor, in functie de nivelul din arbore (LCA-urile de pe un nivel mai jos aflandu-se inaintea celor de pe un nivel mai ridicat). In continuare, vom parcurge LCA-urile in ordinea sortata. Pentru a rezolva problema, avem acum 2 posibilitati:
- Vom renumerota nodurile conform unei parcurgeri in adancime (DF), astfel incat toate nodurile din subarborele oricarui nod i sa formeze un interval de numere consecutive. Apoi vom tine un arbore de intervale pentru aceste numere. In arborele de intervale vom memora daca un nod (identificat prin numarul asociat lui din cadrul parcurgerii DF) a fost eliminat din arbore sau nu. Pentru fiecare LCA, in ordinea precizata mai sus, vom verifica daca cel putin unul din cele 2 noduri al caror LCA este a fost deja eliminat din arbore. Daca nu a fost eliminat nici unul, vom selecta LCA-ul acestora ca oras ce va fi bombardat si vom marca ca intreg intervalul de numere corespunzator subarborelui LCA-ului a fost eliminat din arbore. Complexitatea acestei variante este O(K*logN), plus complexitatea determinarii celor K LCA-uri (care ar putea fi O(N*logN + K*logN)).
- A doua varianta nu mai necesita o renumerotare si utilizarea unui arbore de intervale, insa mentine ideea de a memora pentru fiecare nod daca acesta a fost eliminat sau nu din arbore. Parcurgem LCA-urile si verificam pentru fiecare daca cel putin unul din cele 2 noduri din perechea de noduri pentru care a fost calculat LCA-ul a fost deja eliminat din arbore. Daca nici unul din cele 2 noduri nu a fost eliminat din arbore, vom selecta LCA-ul ca fiind oras ce va fi bombardat si apoi vom efectua o parcurgere DF pentru a marca toate nodurile din subarborele acestuia ca fiind eliminate. Optimizarea importanta este ca daca, in cadrul acestei parcurgeri, intalnim un nod deja marcat anterior ca fiind eliminat, nu vom parcurge subarborele acestuia. In felul acesta, fiecare nod este marcat ca find eliminat cel mult o singura data, iar complexitatea acestei etape este O(K + N).
Swap
Vom construi un o permutare P a multimii {1,...,N}, asociata primului sir (N este lungimea fiecaruia din cele 2 siruri). Pentru fiecare caracter x din primul sir, vom calcula al catelea caracter de tipul respectiv este in cadrul primului sir (acest lucru se poate realiza usor in O(N)). Apoi vom construi permutarea P in felul urmator: pentru fiecare caracter x, pentru care stim ca este al y-lea caracter de tipul sau si care se afla pe pozitia i, vom seta valoarea lui P[i] ca fiind egala cu pozitia pe care se afla cel de-al y-lea caracter egal cu x din cel de-al doilea sir. Numarul de operatii swap necesare este egal cu numarul de inversiuni ale permutarii P. Acest numar poate fi determinat eficient in mai multe feluri: folosind mergesort (sortare prin interclasare), arbori de intervale, arbori indexati binar, impartirea in grupe de cate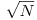 etc.
etc.
Obj
1expr
Cc
Problema cere determinarea unui cuplaj de cost minim, intr-un graf bipartit complet. Aceasta se poate realiza folosind un algoritm de flux maxim de cost minim sau, mai rapid, folosind algoritmul Ungar.
Joc3
Problema este cunoscuta sub numele de "staircase Nim".
Geometry
Itree
Hprob
Nodiv
Arbore de cicluri
Gandaci Java
Problema cere determinarea unui cuplaj maxim intr-un graf bipartit. Algoritmii "standard" pentru determinarea unui cuplaj maxim sunt prea lenti pentru limitele date, de aceea este necesara folosirea unei optimizari, cunoscuta ca algoritmul Hopcoft-Karp (aici gasiti o implementare in Python a acestui algoritm).
Roy-Floyd
Se aplica algoritmul Roy-Floyd standard, la care se adauga un criteriu suplimentar: in cazul in care se gaseste un drum de distanta egala cu distanta minima curenta, dar avand un numar mai mare de strazi, se va alege drumul respectiv.
Biomech
Expresii min-max
Expresia data poate fi evaluata folosind o metoda de complexitate liniara (O(N)). Pentru simplificarea explicatiilor, vom considera ca intreaga expresie este incadrata intr-o pereche de paranteze. Se parcurge expresia de la stanga la dreapta si se va mentine o stiva cu operatorii neevaluati inca, cu rezultate partiale si cu paranteze deschise. Cand se inalneste un operator, acesta se adauga in stiva. Cand se intalneste un operand si in varful stivei este un operator, se efectueaza operatia respectiva (caci in stiva se va gasi si cel de-al doilea operand): adica se elimina din stiva operatorul si cel de-al doilea operand si se pune in varful stivei rezultatul operatiei. Cand se intalneste un operand si in stiva se afla o paranteza deschisa, operandul se pune in varful stivei. La intalnirea unei paranteze inchise vom evalua toate operatiile pana la prima paranteza deschisa din stiva. Apoi vom inlocui paranteza deschisa cu rezultatul evaluarii si, daca pe nivelul urmator din stiva se gaseste un operator, atunci efectuam operatia. La final, in varful stivei vom avea rezultatul expresiei.
