Solutii Winter Challenge 2020

Solutia problemei Hidden Points

Pentru 80 de puncte:

Cautam binar, prin query-uri cu drepte verticale (orizontale), si gasim toate valorile Xj (Yk) pentru care exista macar un punct i ascuns cu coordonata Xi (Yi) egala cu Xj (Yk). Sa zicem ca am obtinut u (v) valori distincte de Xj (Yk), adica 0 ≤ j < u (0 ≤ k < v). Pana acum, am facut O(n*(log(Y_MAX) + log(X_MAX))) query-uri.

Acum avem u * v puncte candidat: Fiecare pereche (j, k) ne spune ca (Xj, Yk) poate fi unul din punctele ascunse. E clar ca punctele ascunse formeaza o submultime a punctelor candidat.

Sa ne alegem un unghi random si sa trasam o dreapta d la acel unghi, care trece, sa zicem, prin origine. Prin fiecare punct candidat Pt, ducem dreapta paralela cu d, pe care o notam cu dt. Sortam punctele candidat dupa distanta intre d si dt. Deoarece unghiul ales este random, este o sansa foarte mare ca dreptele consecutive (in ordinea sortarii) sa se afle la o distanta relevanta. In caz ca distanta intre doua drepte este mai mica decat epsilon = 10-6, alegem alt unghi.

Prin O(n*log(n)) query-uri cu drepte paralele cu d, putem determina precis care sunt acele dt care contin punctele ascunse. Algoritmul poate fi implementat cu o functie recursiva care primeste intervalul [st, dr) de indici ale dreptelor candidat, si apeleaza fiii [st, (st + dr) / 2), [(st + dr) / 2, dr) doar daca afla, prin query, ca exista macar un punct ascuns pentre candidatii de la st la dr-1.

Desi, in practica, solutia este foarte eficienta ca numar de query-uri, iar complexitatea timp, data de sortarea candidatilor, este O(n2 * log(n)), e nevoie de query-uri pe numere reale pentru a diferentia intre dreptele candidat, deci nu obtine punctajul maxim.

Pentru 100 de puncte:

Putem să ne folosim de căutarea binară şi drepte verticale la query-uri pentru a găsi fiecare dreaptă verticală pe care se află puncte şi numărul acestora (folosim O(n*log(X_MAX)) query-uri). Acum pentru fiecare Xi trebuie să găsim unde se află fiecare punct. Putem să aplicăm o strategie similară şi să căutăm binar punctele astfel: Căutăm binar cel mai mic Y care are un punct nedescoperit încă, iar la query folosim punctele (Xi + 1, 0) şi (Xi, Y). Astfel punctele din stânga dreptei ori au fost descoperite ori au abscisa egală cu Xi (acest pas foloseşte O(n*log(Y_MAX)) query-uri).

Raspunsul la query nu trebuie decat comparat cu numarul de puncte cunoscute deja care se afla sub dreapta. E suficient sa verificam, intr-o maniera brute-force, care dintre punctele cunoscute se afla sub dreapta. Complexitatea ca timp este O(n2*(log(X_MAX) + log(Y_MAX))).

Solutia problemei Beyond the Wall

Ce este dualizarea?

Dualizarea este un concept folosit în geometrie prin care putem să transformăm un punct într-o dreaptă şi invers astfel încât oricărei teoreme din planul primal îi corespunde o teoremă din planul dual. Pentru mai multe detalii vă recomand următoarele linkuri: wikipedia , Point‐Line Duality

O proprietate a spaţiului dual este că dacă în plan primal un punct A se află sub dreapta d atunci în plan dual punctul D se află sub dreapta a (D este punctul obţinut din dreapta d, iar a este dreapta obţinută din punctul A)

Demonstraţie:

În primul rând un punct A(xA, yA) se află sub dreapta d: y = mx + b doar dacă mxA - yA + b > 0
Să persupunem că avem punctul A de coordonate (xA, yA) şi dreapta d de ecuaţie y = mx+b astfel încât X se află sub dreaptă.
Deci mxA - yA + b > 0.
În plan dual A devine a cu ecuaţia: y = xAx - yA iar d devine D de coordonate (m, -b).
Înlocuind în formula de mai sus obţinem:
xAm - yA - (-b) > 0
xAm - yA + b > 0 (echivalentă cu cea din planul primal)

Pentru 65 de puncte:

În primul rând vom aplica principiul dualizării şi obţinem q puncte şi n drepte. Acum pentru fiecare punct trebuie să numărăm câte drepte trec pe deasupra lui. Mergând de la stânga la dreapta pe axa Ox şi sortând dreptele după înălţimea în acel X vom observa că există maxim n2 permutări ale acestor drepte. Acest fapt se întâmplă deoarece oricare două drepte se intersectează maxim o dată. Putem să determinăm punctele în care fiecare pereche de drepte se intersectează şi să le sortăm. Astfel putem să construim permutările în O(n2 * log(n)). Parcurgem punctele de la stânga la dreapta şi facem swap-urile necesare în permutare. Pentru fiecare punct putem să căutăm binar câte drepte se află deasupra lui deoarece acestea vor fi sortate după înălţime.
Pentru 65 de puncte este nevoie însă de încă o optimizare. Cum X_MAX este destul de mic se poate folosi Count Sort pentru a reduce complexitatea de generare a permutărilor la O(n2). Detaliile rămân ca tema cititorului.

Pentru 100 de puncte:

Pentru a obţine punctaj maxim avem nevoie de o structură de date care să gestioneze în mod eficient punctele. Putem să folosim un Quad-Tree care la fiecare pas împarte planul în 4 cadrane cu număr aproximativ egal de puncte. În fiecare nod reţinem câte puncte se află în cadranul corespunzător. Complexitatea pentru construcţia arborelui este O(n * log(n)) dacă la fiecare pas este împărţit doar cel mai mic dreptunghi care conţine punctele din nodul actual. Pentru query observăm că o dreaptă nu poate să taie mai mult de 3 cadrane deci la fiecare pas putem să eliminăm cel puţin unul dintre acestea şi să mergem recursiv în cadranele care nu se află complet sub dreaptă. Complexitatea acestui query respectă formula T(n) = 3 * (T(n / 4)) + O(1) deoarece merg recursiv în maxim 3 cadrane care au aproximativ n / 4 puncte, deci, din Master Theorem, T(n) = O(nlog43). Complexitatea finală este O(n * log(n) + q * nlog43).
Pentru 100 de puncte trebuie să mai facem o optimizare. Putem să generăm răspunsurile pentru fiecare query în plan dual. Astfel în Quad-Tree vom pune punctele de query şi pentru fiecare dreaptă o să facem lazy update pe cadranele complet aflate sub dreaptă. La final trebuie decât să mai parcurgem o dată arborele pentru a extrage răspunsul pentru fiecare query. Astfel complexitatea finală devine O(n * log(n) + n * qlog43). Deşi complexitatea teoretica pare că este destul de mare, acest algoritm se comportă foarte bine în practică.

Solutia problemei Battle of the Blackwater

Pentru orice numar x exista 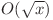O(\sqrt{x}) valori distincte la impartirea x / i. Astfel vor exista 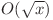O(\sqrt{x}) intervale pentru i unde fiecare interval are asociat valoarea x / i. De exemplu pentru x = 16 exista intervalele (1-1), (2-2), (3-3), (4-4), (5-5), (6-8), (9-16) unde valorile asociate vor fi pe rand 16, 8, 5, 4, 3, 2, 1. Putem folosi aceasta observatie pentru a optimiza calculul aportului fiecarui numar pe fiecare pozitie in care ar rezulta in urma permutarii circulare. Deci daca vectorul nostru are forma [x,x,x,16,x,x,x,x,x,x,x] si stim ca are intervalele de mai sus pentru permutarea circulara la stanga de 3 ori are asociat intervalul 1-1 cu valoarea 16, pentru permutarea de 2 ori are valoarea 8, pentru permutarea circulara o data are valoarea 5, pentru nicio permuare are valoarea 4, pentru permutarea circulara la dreapta o data (echivalenta cu permutare la stanga de 10 ori) valoarea este 3, iar de acum inainte vor urma intervale mai lungi cu acelasi rezultat, pentru permutarile la dreapta de 2, 3 sau 4 ori 16 va contribui cu 2 iar pentru permutarile la dreapta de 5, 6 sau 7 va contribui cu 1. Asadar se poate aplica smenul lui mars pentru a adauga pe un interval o valoare si se poate rezolva problema in O(n * \sqrt{valmax}) .

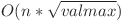Solutia problemei Cmmdcgame

Cunostinte necesare: teorema Sprague-Grundy, nimber-uri. Autorul problemei recomanda acest tutorial

Conform teoremei Sprague-Grundy, jocul din enunt se poate reduce la un joc de nim pe o singura gramada (nimber-ul jocului). Cum adunarea pe nimber-uri corespunde operatiei XOR, si suma a doua jocuri, in acest sens, este jocul ce rezulta prin jocul in paralel a celor doua jocuri, se poate arata ca este suficient sa calculam nimber-ul fiecarei gramezi (oras, in enunt), apoi sa calculam XOR-ul lor, si apoi sa vedem daca rezultatul este 0 (in care caz castiga al doilea jucator) sau nu (in care caz castiga primul jucator).

Care este nimber-ul unei gramezi (oras)? Stim ca nimber-ul unei stari dintr-un joc este egal cu cel mai mic nimber la care nu putem ajunge printr-o mutare din acea stare. Mai intai sa ne gandim la nimber-ul unei gramezi de marime prima (sau 1). Din aceasta stare putem sa mergem in oricare marime mai mica de gramada -- inclusiv toate marimile prime (sau 1) mai mici. Asta implica ca numerele prime (si 1) au nimber-uri strict crescatoare. Ba chiar, daca jocul ar permite sa mergem doar prin gramezi de marime prima (sau 1), atunci 1 ar avea nimber-ul 0, 2 nimber-ul 1, 3 nimber-ul 2, 5 nimber-ul 3, 7 nimber-ul 4 si asa mai departe. Sa presupunem pe moment ca aceste atribuiri de nimber-uri sunt corecte. Care ar fi atunci nimber-ul unui numar compus? Este clar ca dintr-un numar compus putem muta in toate numerele prime (si 1) mai mici ca cel mai mic factor prim al numarului nostru. Totodata nu putem muta in niciun numar care impartaseste acest factor prim minim (ca acel numar ar fi necoprim cu numarul actual). Asta ne arata ca nimber-ul unui numar compus este egal cu nimber-ul celui mai mic factor prim al numarului (acest fapt se poate demonstra riguros prin inductie).

Astfel, concret, pentru a rezolva problema, calculam, cu ajutorul unui ciur (analog cu ciurul lui Eratostene), pentru fiecare marime posibila de oras, valoarea f(x), egala cu cel mai mic factor prim al lui x, respectiv i(x), egala cu indicele lui x ca numar prim (sau 1), adica i(1) = 0, i(2) = 1, i(3) = 2, i(5) = 3, i(7) = 4, etc. Atunci, calculam XOR-ul valorilor i(f(x)) pentru toate marimile x de orase, si afisam ca primul jucator (adica Daenarys) castiga daca si numai daca aceasta valoare este nenula.