Revizia anterioară Revizia următoare
Teoria jocurilor
(Categoria Teoria jocurilor, Autor Filip Cristian Buruiana)
- Capitole
- Notiuni de baza
- Jocul NIM
- Numere Sprague-Grundy
- Adunarea jocurilor
- w-numere
- Aplicatii si probleme
Aplicatii, probleme
In continuare vom analiza cateva aplicatii si probleme in care se aplica teoria si teoremele prezentate in capitolele precedente.
1. Game, concursul national Bursele Agora, 2004
Fie N gramezi de pietre si doi jucatori care muta alternativ. O mutare consta din alegerea unei gramezi si eliminarea unei singure pietre sau a unui numar prim de pietre din gramada aleasa. Castiga jucatorul care ia ultimele pietre. Sa se precizeze care din cei doi jucatori va castiga.
Jocul de mai sus este similar cu jocul de NIM, numai ca aici nu putem lua oricate pietre dintr-o gramada, ci doar o singura piatra sau un numar prim de pietre. Pentru a rezolva problema, facem urmatoarea observatie: jocul cu mai multe gramezi respecta proprietatile unei adunari de tip xor a jocurilor cu o singura gramada, deoarece la fiecare pas jucatorul care urmeaza trebuie sa isi aleaga exact un joc (o gramada) si sa faca o mutare in jocul respectiv. Conform teoremei, rezulta ca trebuie sa determinam valoarea mex pentru o gramada cu x pietre, si apoi sa facem suma-xor a valorilor corespunzatoare marimilor celor N gramezi. In cazul in care suma-xor este diferita de 0 va castiga jucatorul care muta primul, iar in caz contrar va castiga celalalt jucator.
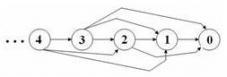 Mai ramane de calculat valoarea mex pentru o gramada cu x pietre. Putem construi un graf orientat, aciclic, in care nodul numerotat cu x, x ≥ 0, reprezinta o gramada de dimensiune x. In acest graf va exista arc de la x la y doar daca x - y este egal cu 1 sau este un numar prim. Astfel, un arc reprezinta o posibila mutare in jocul dat.
Mai ramane de calculat valoarea mex pentru o gramada cu x pietre. Putem construi un graf orientat, aciclic, in care nodul numerotat cu x, x ≥ 0, reprezinta o gramada de dimensiune x. In acest graf va exista arc de la x la y doar daca x - y este egal cu 1 sau este un numar prim. Astfel, un arc reprezinta o posibila mutare in jocul dat.
Vom incerca sa calculam valorile Sprague-Grundy corespunzatoare nodurilor acestui graf. In tabelul de mai jos sunt prezentate aceste valori pentru primele noduri ale grafului.
| nod | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SG | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 |
Se poate demonstra prin inductie dupa n ca valoarea asociata nodului n este n modulo 4. Pentru 0 ≤ n ≤ 3 afirmatia este adevarata. Presupunem afirmatia adevarata pentru orice m < n. Din gramada de n obiecte pot fi luate unul, doua sau trei obiecte, deci valoarea pentru n nu poate fi niciuna din valorile pentru n-1, n-2 si n-3. Valoarea n modulo 4 este deocamdata cea mai mica valoare care nu este inca eliminata si poate corespunde gramezii cu n obiecte. Este usor de aratat ca aceasta valoare nu va fi eliminata. Presupunem prin reducere la absurd ca valoarea ar fi eliminata, deci putem alege un numar prim p de obiecte din cele n astfel incat (n-p) modulo 4 = n modulo 4, echivalent cu p modulo 4 = 0, fals, deoarece p era un numar prim. In concluzie, afirmatia pentru n este adevarata si, conform principiului inductiei matematice, este adevarata pentru orice n numar natural. In concluzie, valoarea Sprague-Grundy pentru nodul n este n modulo 4.
Codul C++ care rezolva problema este prezentat mai jos:for (i = 1, S = 0; i <= N; ++i)
S ^= (x[i] % 4);
if (S != 0) printf("Primul jucator castiga");
else printf("Al doilea jucator castiga");3. Cartonase, concursul national .campion 2007-2008, clasele XI-XII
Notiuni de baza | Jocul NIM | Numere Sprague-Grundy |
Adunarea jocurilor | w-numere | Aplicatii si probleme
