| Fişierul intrare/ieşire: | aria.in, aria.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de |  Simoiu Robert •SpiderMan |
| Timp execuţie pe test | 0.2 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Poti vedea testele pentru aceasta problema accesand atasamentele.Vezi solutiile trimise | Statistici
Aria
Dându-se un poligon convex cu N vârfuri, să se determine aria acestuia.
Date de intrare
Fişierul de intrare aria.in conţine pe prima linie numărul de puncte N, date în ordine trigonometrică, iar pe urmatoarele N linii 2 numere reale, xi şi yi, care reprezintă coordonatele punctului i.
Date de ieşire
Fişierul de ieşire aria.out va conţine un singur număr reprezentând aria poligonului dat.
Restricţii
- 1 ≤ N ≤ 100 000
- -1 000 000 ≤ xi, yi ≤ 1 000 000
- Rezultatul se va afişa cu o precizie de 10-5.
Exemplu
| aria.in | aria.out | Explicaţie |
|---|---|---|
| 4 -2 -2 2 -2 2 2 -2 2 | 16 | Aria poligonului dat este de fapt aria dreptunghiului din figură.
|
Indicaţii de rezolvare
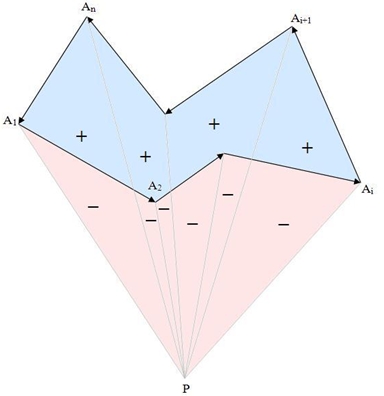
Desi problema are ca date de intrare poligoane convexe, rezolvarea de mai jos este valabila pentru orice tip de poligoane. Pentru a calcula aria unui poligon A1A2A3..An, vom considera un punct P arbitrar ales în plan. Vom "împărţi" poligonul în triunghiuri de forma PAiAi+1 (considerăm că A1 = An+1) şi vom calcula "aria cu semn" Ti a fiecărui triunghi (în formula ariei nu vom folosi funcţia de valoare absolută). Distingem în acest moment două cazuri:
- Poligonul are vârfurile orientate trigonometric. Pentru fiecare latură "spre dreapta", aria Ti corespunzătoare va fi negativă, iar pentru fiecare latură "spre stânga", aria Ti corespunzătoare va fi pozitivă.
- Poligonul are vârfurile orientate antitrigonometric. Pentru fiecare latură "spre dreapta", aria Ti corespunzătoare va fi pozitivă, iar pentru fiecare latură "spre stânga", aria Ti corespunzătoare va fi negativă.
În ambele cazuri, efectuând suma algebrică a ariilor Ti vom obţine aria poligonului (deoarece ariile negative vor "anula" zonele corespunzătoare ariilor pozitive care se află în afara poligonului).
Dacă alegem punctul P(0, 0), fiecare arie Ti devine:
![\begin{math}T_{i} = \frac{1}{2}\cdot \left\left|\begin{array}{ccc}
\ 0 & 0 & 1\
x_i & y_i & 1\
x_{i+1} & y_{i+1} & 1\end{array}\right|\right = \frac{1}{2}\cdot \left(x_i\cdot y_{i+1}-x_{i+1}\cdot y_i\right)
\end{math}](http://www.infoarena.ro/static/images/latex/5a93b9a60991eae7dba16a3a783c18bf_16.50018pt.gif "\begin{math}T_{i} = \frac{1}{2}\cdot \left\left|\begin{array}{ccc}
\ 0 & 0 & 1\
x_i & y_i & 1\
x_{i+1} & y_{i+1} & 1\end{array}\right|\right = \frac{1}{2}\cdot \left(x_i\cdot y_{i+1}-x_{i+1}\cdot y_i\right)
\end{math}")
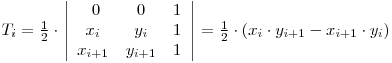
Formula finală devine:
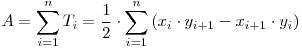
Această formulă reprezintă "aria cu semn" a poligonului (o arie pozitivă indică parcurgerea vârfurilor în ordine trigonometrică, iar o arie negativă, parcurgerea in ordine antitrigonometrică). O sursă care se bazează pe această soluţie obţine 100 puncte.
Aplicaţii
O primă aplicaţie ar fi coliniaritatea a N puncte. Pentru ca N puncte să fie coliniare, trebuie ca aria determinată de poligonul asociat acestora să fie 0. O altă aplicaţie drăguţă este următoarea : dacă un punct se află în interiorul unui poligon convex. Soluţia presupune calcularea ariei cu semnn a triunghiurilor determinate de oricare 2 puncte de pe acest poligon şi punctul căutat. Dacă toate ariile au acelasi semn (+ sau -), atunci punctul se află în interiorul poligonului.
Printre problemele care folosesc aria unui poligon se numără :
