Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2015-02-22 16:05:04.
Revizia anterioară Revizia următoare

Soluţii ONIS 2015, Runda 1

Por Costel şi Azerah

Solutia cea mai la indemana la problema aceasta se bazeaza pe metoda programarii dinamice:
Calculam:

dp[i][0] = numarul de submultimi cu suma numerelor para cu primele i numere din sir
dp[i][1] = numarul de submultimi cu suma numerelor impara cu primele i numere din sir

Cazul de baza:

dp[0][0] = 1 (submultimea vida)
dp[0][1] = 0

Relatia de recurenta:

Daca numarul v[i] este par:
- dp[i][0] = 2 * dp[i-1][1]
- dp[i][1] = 2 * dp[i-1][1]
Daca numarul v[i] este impar:
- dp[i][0] = dp[i-1][0] + dp[i-1][1]
- dp[i][1] = dp[i-1][0] + dp[i-1][1]

Complexitate: 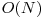$O(N)$

Insa, la o inspectie mai amanuntita a dinamicii sau dupa un rationament combinatoric descoperim ca:

Daca exista numai numere pare in sir, raspunsul este 2ⁿ - 1
Altfel este 2^n-1 - 1

Acum, daca ignoram citirea sirului, complexitatea este 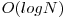$O(log N)$

Por Costel şi Algoritmul

Stim ca aloritmul va lua cel putin doua iteratii pentru ca se garanteaza ca exista cel putin o muchie care iese din nodul 1. Pentru ca algoritmul lui Por Costel sa se termine in doua iteratii, trebuie ca doar la prima iteratie sa se produca relaxari ale muchiilor (modificari ale vectorului d). Cand se intra in iteratia a doua trebuie ca in vectorul d sa existe deja valorile drumurilor minime pentru a nu se produce nicio modificare, variabila ok sa ramana cu valoarea 1 si sa nu se mai intre in while a treia oara.

Pentru a rezolva problema sunt necesare niste cunostiinte generale despre problema drumurilor minime intr-un graf, de exemplu, faptul ca reuniunea drumurilor minime din nodul x catre toate celelalte noduri formeaza un arbore (arborele partial al drumurilor minime din x). Observam ca daca muchiile din acest arbore sunt parcurse in ordinea unei parcurgeri din nodul x (DFS sau BFS sau orice fel de parcurgere), drumurile minime se vor propaga complet. Deci solutia este o astfel de ordonare a N-1 muchii care formeaza un arbore partial de drumuri minime din nodul 1 iar restul de @M-N+1 muchii pot fi interclasate cu acestea in orice fel.

Pentru a construi un arbore partial de drumuri minime din nodul 1, trebuie sa aplicam un algoritm de drum minim. O solutie este chiar Bellman-Ford dar acesta are complexitate O(N*M) chiar si daca il codezi mai bine ca Por Costel. Pentru ca muchiile din graf au cost pozitiv, drumurile minime se pot calcula folosind algoritmul lui Dijkstra

Complexitatea: 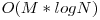$O(M*logN)$

Testul pe care pica Bellman-Ford:

Muchiile 1 -> 2, 2 -> 3, 3 -> 4... N-1 - > N, toate de cost 1
Muchiile 1 -> 3, 1 -> 5, 1 -> 7....1 ->N-1/N, toate de cost 10

Este nevoie de un shuffle foarte norocos al muchiilor din nodul 1 pentru ca algoritmul sa mearga bine.

Por Costel şi Bujor

Constatarea cheie aici este ca daca inmultim matricele B si P obtinem matricea I cu semnificatia: I[i][j] = total expected winnings pentru Bujor in casino-ul i, in ziua j.
Observam ca matricele I care satisfac cerinta finala sunt matricele permutare, printe care se numara si matricea identitate I_n. Deci matricea P poate fi inversa matricei B. Matricea B este garantat inversabila deoarece se garanteaza ca exista solutie la problema (Ecuatia matriceala B*P = I cu det(I) nenul are solutie doar daca det(B) este si el nenul)

Inversa matricei se poate calcula in 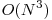$O(N^3)$ cu o variatie a algoritmului lui Gauss care se cheama eliminare Gauss-Jordan. Prin inmultiri de linii cu constante, si scadere de linii din alte linii, putem aduce matricea B la matricea I_n. Atunci operatiile pe care le-am efectuat sunt echivalente cu inmultirea cu matricea B^-1. Daca retinem aceste operatii si le aplicam pe matricea I_n, vom obtine matricea B^-1. Mai multe explicatii/informatii se gasesc si aici

Por Costel şi Comisia de Cenzură

Problema aceasta poate fi impartita in doua subprobleme:

Aflarea pozitiilor dintr-un text pe care apar cuvintele dintr-un dictionar
Dandu-se un numar de intervale pe axa Ox, si costuri pe fiecare pozitie de pe axa Ox sa se gaseasca o acoperire a intervalelor (fiecare interval sa aibe cel putin un punct care il acopera) de cost minim.

Subproblema 1

Aceasta problema admite mai multe solutii, insa cea de complexitate optima se foloseste de un automat Aho-Corasick. Va rugam sa-l studiati inainte de a citi mai departe. Vom numi nod terminal un nod din Aho-Corasick in care se termina un cuvant din dictionar. Fiecare nod din automat va avea un vector dinamic mathces, o lista cu indici ai prefixelor din text pentru care cuvantul determinat de acest nod (mai precis de drumul de la radacina la acest nod) este sufix. Atunci cand 'trecem textul prin automat' incarcam fiecare indice i din text (care reprezinta prefixul care se termina la pozitia i) in vectorul matches al nodului la care am ajuns la momentul respectiv. Acesta va fi cel mai lung prefix al unui cuvant din dictionar care este sufix al unui prefixului i al sirului. Pentru a afla toate prefixele din dictionar care sunt sufixe ale acestui prefix i, este suficient sa copiem continutul vectorului matces al nodului curent in vectorii matches ai nodurilor in care ajungem urmarind pointerul de nepotrivire fail. Putem scoate pozitiile de potrivire ale cuvintelor din vectorii matches ale nodurilor terminale.

Atentie ! Aici se poate cadea intr-o capcana. Problema garanteaza ca numarul de aparitii ale cuvintelor din dictionar in text nu depaseste 10⁴, dar problema nu garanteaza pentru numarul de aparitii ale prefixelor cuvintelor din dictionar.

Daca avem textul T: aaaaaaa
si un cuvant un dictionar C: aaaaaaa
Numarul de aparitii ale lui C in T este 1 dar numarul de aparitii ale unui prefix al lui C in T este 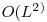$O(L^2^)$ unde L este lungimea lui C. Urmarind procedeul de mai sus putem da peste o explozie in vectorii matches, dimensiunea lor find de ordinul 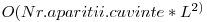$O(Nr.aparitii.cuvinte*L^2^)$ . Pentru a remedia acest lucru, vom mentine in fiecare nod o valoare booleana care ne spune daca urmarind pointerul fail mai putem ajunge la un nod terminal. Daca aceasta valoare este false, nu mai copiem continutul vectorului matches al nodului curent mai departe.

Pana acum avem complexitate 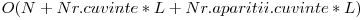$O(N + Nr.cuvinte*L + Nr.aparitii.cuvinte*L)$ unde L este lungimea maxima a unui cuvant.

Subproblema 2

Problema aceasta se trateaza prin programare dinamica. Este clar ca putem inlatura intervalele care contin alte intervale. Dinamica de mai jos functioneaza si daca nu facem aceasta reducere, dar o sa consideram ca o facem pentru ca simplifica explicatia:

Intervalele sunt acum lipsite de parantezari deci o sortare dupa capatul stanga reprezinta si o sortare dupa capatul dreapta. Indexam intervalele dupa aceasta ordine. Al i-lea interval este cel cu al i-lea capat stanga. Deoarece alegand o pozitie i din text acoperim o secventa continua de astfel de intervale, putem construi dinamica:

dp[i] = costul minim de a acoperi primele i intervale.

Parcurgem pozitiile de pe axa Ox de la stanga la dreapta. Presupunem ca stim configuratia de intervale la care suntem la pozitia i. Aceasta va fi o secventa continua de intervale - [l..r], unde l este cel mai din stanga interval iar r este cel mai din dreapta. intervalele [1..l-1] trebuiau acoperite cu pozitii mai mici decat aceasta, nu mai avem cum sa le acoperim de aici. Asadar, este necesar si suficient sa updatam dp[k] = min (dp[k], dp[l-1] + v[i]) pentru orice l ≤ k ≤ r. Mai jos aveti codul pentru a intelege mai bine:

int get_answer (vector<pair<int,int> > intervals)
{
    sort (intervals.begin(), intervals.end());
 
    for (int i = 0; i < intervals.size(); ++i)
    {
        bal[intervals[i].first][0].push_back(i+1);  //bal[i][0] - lista de intervale care incep la pozitia i
        bal[intervals[i].second][1].push_back(i+1); //bal[i][1] - lista de intervale care se termina la pozitia i
    }
 
    for (int i = 1; i <= intervals.size(); ++i)
        dp[i] = inf;
 
    dp[0] = 0;
    int not_present = 0;
    int present = 0;
 
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 0; j < bal[i][0].size(); ++j)
        {
            present = max (present, bal[i][0][j]);
        }
 
        for (int j = not_present+1; j <= present; ++j)
        {
            dp[j] = min (dp[j], dp[not_present] + v[i]);
        }
 
        for (int j = 0; j < bal[i][1].size(); ++j)
        {
            not_present = max(not_present, bal[i][1][j]);
        }
    }
 
    return dp[intervals.size()];
}

Dar stati, complexitatea nu devine cumva 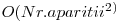$O(Nr.aparitii^2^)$ ? De fapt, fiecare interval este parcurs si updatat atata timp cat el contine pozitia curenta. Intervalele sunt de lungime maxim 100 si complexitatea acestei parti este de fapt $O(N + Nr.aparitii*L)$ .

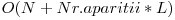Tinem sa-l felicitam pe Popa Andrei •andreiiii, care a reusit sa rezolve aceasta problema in mod specataculos in ultimul minut.

Por Costel şi Cifrul

Solutia la aceasta problema se foloseste de principiul includerii si excluderii. Vom numara si aduna numarul de coduri care deschid seiful datorita apropierii de primul cod din cele M, de a al doilea cod, de al treilea cod.. apoi le vom scadea pe cele care sunt apropiate simultan de primul si al doilea, de primul si de al treilea, de al doilea si de al treilea.. etc.

Presupunand ca am fixat o configuratie de coduri si stim pentru fiecare i nr[i] = numarul de celule care apartin intersectiei intervalelor corespunzatoare rotitei i. Numarul de coduri 'apropiate' de fiecare din codurile din configuratie este data de nr[1]*nr[2]*nr[3]*..nr[N].

Tot ce trebuie sa facem este construim intersectiile pentru fiecare configuratie, pe fiecare rotita, sa calculam rezultatul si sa il adunam sau scadem din solutie.
Lucrul care poate sa nu fie evident la prima vedere este ca desi intersectia a X intervale pe o axa este un interval (sau multimea vida), pe un cerc, ea nu este interval. Ea poate consta si din M intervale disjuncte. De exemplu:
----------- -----------
------- ---------------
---- ------------------

Cel mai sigur mod de a implementa functia de intersectie este de a ne inchipui ca suntem de fapt pe o axa necirculara. Astfel, intervalele (x,y) cu x > y le despartim in [x,k-1] si [0,y]. Acum, intersectia a X intervale disjuncte cu Y intervale disjuncte este reuniunea intersectiilor fiecare perechi de intervale (a,b) cu a din X si b din Y. Adica functia de intersectie o putem scrie asa:

void intersect (vector<pair<int,int> > X[], vector<pair<int,int> > Y[], vector<pair<int,int> > intersection[])
{
    for (int i = 1; i <= n; ++i)  // pentru fiecare rotita
    {
        for (int j = 0; j < X[i].size(); ++j)
        {
            for (int h = 0; h < Y[i].size(); ++h)
            {
                int front = max (X[i][j].first, Y[i][h].first);
                int end = min (X[i][j].second, Y[i][h].second);
 
                if (front <= end)
                    intersection[i].push_back(make_pair(front, end));
            }
        }
    }
}

Noi vom intersecta mereu o multime de intervale cu un interval de forma (x-D,x+D) care se va transpune in 1 sau 2 intervale necirculare, adica Y[i].size() va fi mereu 1 sau 2. Complexitatea functiei de mai sus este astfel 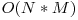$O(N*M)$ .

Acum, modul in care vom parcurge intersectiile va dicta complexitatea finala. Daca pur si simplu iteram prin cele 2^M configuratii iar pentru fiecare configuratie construim intersectia intervalelor din configuratie de la zero, complexitatea va fi 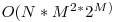$O(N*M^2^*2^M^)$ .

Complexitatea care rezolva problema este 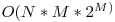$O(N*M*2^M^)$ care poate fi obtinuta prin metoda backtracking, construind treptat intersectia celor M coduri.

Por Costel şi Invazia Extraterestră

Solutia corecta la aceasta problema presupune cunoasterea structurii de date Arbore de intervale.

Problema se poate rezolva mentinand in fiecare nod al unui arbore de intervale o structura de date auxiliara care sa poata sa raspunda rapid la inserari, stergeri si query-uri de minim (de exemplu, heap). Insa, cum operatiile de inserare si stergere la problema aceasta sunt parantezate corect, este indeajuns o stiva.

Cand primim o inserare, descompunem intervalul primit in cele logN noduri corespunzatoare din arborele de intervale, iar in varful stivei din fieacre din aceste noduri incarcam min(inaltimea noii nave, varful precedent al stivei). La stergere, luam intervalul asociat ultimei inserari (care il vom memora probabil tot cu ajutorul unei stive) si, din nou, il descompunem in cele logN noduri asociate, pe stivele carora apelam pop()(stergem varful).

De notat este ca problema nu necesita lazy-update, intrucat query-urile sunt punctiforme (nu sunt pe interval). Un query va parcurge pe arborele de intervale un drum de la radacina la o frunza. Daca in fiecare dintre nodurile de pe drum, ne uitam la ce se afla in varful stivei, raspunsul pentru query va fi minimul dintre aceste valori.

Complexitatea este 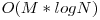$O(M*logN)$

Por Costel şi Livada

Sa consideram o rezolvare prin programare dinamica si o dinamica cu urmatoarea semnificatie:

dp[i][j] = valoarea maxima a unei livezi care contine celula (i,j) si poate contine celule de pe linii ≤ i.

O rezolvare in 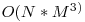$O(N*M^3^)$ este destul de la indemana. Parcurgem liniile de la 1 la i. Presupunand dinamica calculata pentru liniile &l; i

Por Costel şi Meciul

Por Costel şi Perechile

Por Costel şi Pinball

Por Costel şi Semipalindroamele