- Conţinut:
- 0. Introducere
- 1. Arii
- 2. Drepte
- 3. Punct în poligon
- 4. Intersecţii de drepte şi segmente
- 5. Distanţe
- - între linii
- - între segmente şi semidrepte
- - cea mai mică distanţă între două mobile
- 6. Bounding ...
- - ... box
- - ... circle
- 7. Infaşurătoare convexă
- 8. Puncte extreme şi distanţa poligon-linie
- 9. Tangente
- 10. Probleme de concurs
1. Arii
Noţiunea de arie este una de bază în geometria analitică. Este necesară însă o prezentare a diferitelor metode de a calcula ariile in contextul prelucrarii datelor pe calculator.
Aria unui triunghi
În determinarea ariei unui triunghi se poate folosi formula lui Heron:
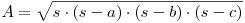
În formulă, s reprezintă semiperimetrul triunghiului, iar a, b, c lungimile laturilor triunghiului. Această formulă apare şi într-o altă formă, mult mai adecvată algoritmilor prin faptul că se evită calcularea lungimii laturilor cu radical:
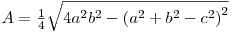
În contextul geometriei vectoriale, modulul produsului vectorial a doi vectori o reprezintă aria paralelogramului cuprins între vectori. Aplicând raţionamentul la triunghiuri, obţinem relaţia:
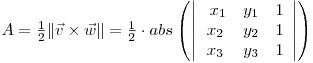
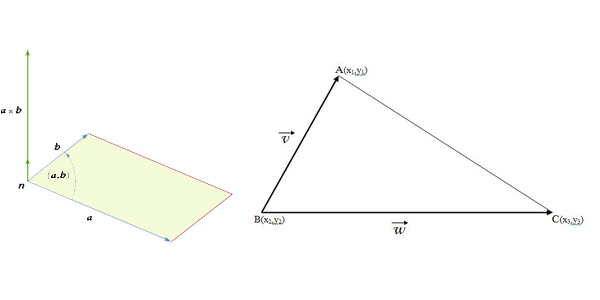
Aria unui patrulater
După cum am văzut în cazul unui triunghi, aria unui paralelogram ABCD este egală cu modulul produsului vectorial al vectorilor reprezentaţi de 2 laturi neparalele.
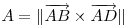
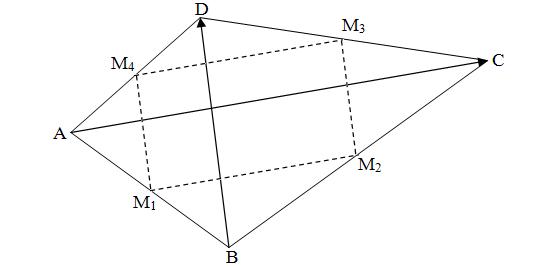
Pentru un patrulater oarecare ABCD, putem considera M1, M2, M3, M4 mijloacele laturilor acestuia. Se poate demonstra că patrulaterul M1M2M3M4 este un paralelogram cu aria jumătate din aria lui ABCD:
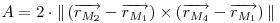
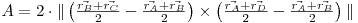
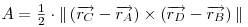
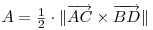
Aria unui poligon
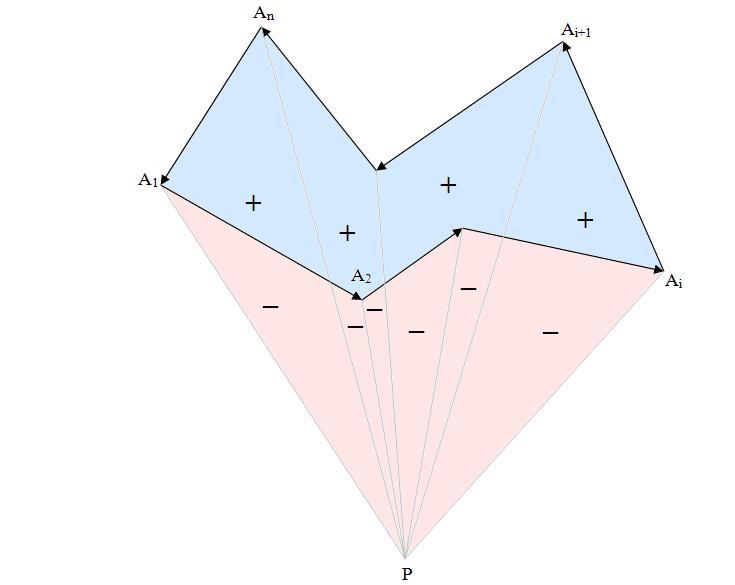
Pentru a calcula aria unui poligon oarecare A1A2A3..An, vom considera un punct P arbitrar ales în plan. Vom "împărţi" poligonul în triunghiuri de forma PAiAi+1 (considerăm că A1=An+1) şi vom calcula "aria cu semn" Ti a fiecărui triunghi (în formula ariei nu vom folosi funcţia de valoare absolută). Distingem în acest moment două cazuri:
- Poligonul are vârfurile orientate trigonometric. Pentru fiecare latură "spre dreapta", aria Ti corespunzătoare va fi negativă, iar pentru fiecare latură "spre stânga", aria Ti corespunzătoare va fi pozitivă.
- Poligonul are vârfurile orientate antitrigonometric. Pentru fiecare latură "spre dreapta", aria Ti corespunzătoare va fi pozitivă, iar pentru fiecare latură "spre stânga", aria Ti corespunzătoare va fi negativă.
În ambele cazuri, efectuând suma algebrică a ariilor Ti vom obţine aria poligonului (deoarece ariile negative vor "anula" zonele corespunzătoare ariilor pozitive care se află în afara poligonului).
Dacă alegem punctul P(0,0), fiecare arie Ti devine:
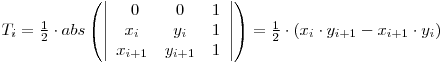
Formula finală devine:
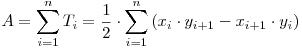
Această formulă reprezintă "aria cu semn" a poligonului (o arie pozitivă indică parcurgerea vârfurilor în ordine trigonometrică, iar o arie negativă, parcurgerea in ordine antitrigonometrică).
