Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2013-09-19 13:25:12.
Revizia anterioară   Revizia următoare  

Eliminare Gaussiană

(Categoria Algoritmi, Autor Petru Trîmbiţaş)

Descriere

Eliminarea Gaussiană este o metodă de rezolvare a ecuaţiilor matriciale de forma 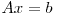Ax=b.
Să presupunem că avem următorul sistem:

\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{pmatrix} * \begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{pmatrix} = \begin{pmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{pmatrix}

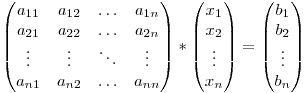
Pentru a rezolva sistemul vom transforma toate elementele de sub diagonala principală a matricei extinse în 0 pentru a putea scrie fiecare necunoscută doar în funcţie de necunoscutele cu indici mai mari.

\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} & b_{1}\\ a_{21} & a_{22} & \ldots & a_{2n} & b_{2}\\ a_{31} & a_{32} & \ldots & a_{3n} & b_{3}\\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} & b_{n} \end{pmatrix} \rightarrow \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} & b_{1}\\ 0 & a'_{22} & \ldots & a'_{2n} & b'_{2}\\ 0 & 0 & \ldots & a'_{3n} & b'_{3}\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & a'_{nn} & b'_{n} \end{pmatrix}

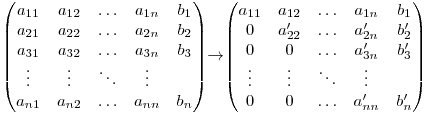
Având matricea sub această formă putem să aflăm uşor fiecare necunoscută din ecuaţia în care necunoscutele cu indici mai mici au coeficientul 0:
\: x_{n}=\frac{b'_{n}}{a'_{nn}}
x_{n-1}=\frac{b'_{n-1}-a'_{n-1n}*x_{n}}{a'_{n-1n-1}}
\vdots
x_{i}=\frac{b'_{i}-\sum\limits_{j=i+1}^n a'_{ij}*x_{j}}{a'_{ii}}

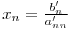
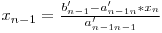
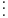
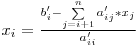
Acum că ştim să aflăm necunoscutele din forma triunghiulară a matricei ne mai rămâne doar să transformăm matricea.
Pentru a transforma matricea în formă triunghiulară vom aplica două operaţii:
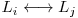L_{i} \longleftrightarrow L_{j} : interschimbarea a două linii
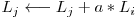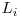L_{j} \longleftarrow L_{j}+a*L_{i} unde L_{i} este o linie a matricei extinse.

De exemplu:

\begin{pmatrix} 2 & 1 & -1 & 8 \ -3 & -1 & 2 & -11 \ -2 & 1 & 2 & -3 \end{pmatrix} \longrightarrow \begin{pmatrix} 2 & 1 & -1 & 8 \ 0 & \frac{1}{2} & \frac{1}{2} & 1 \ 0 & 2 & 1 & 5 \end{pmatrix} \longrightarrow \begin{pmatrix} 2 & 1 & -1 & 8 \ 0 & \frac{1}{2} & \frac{1}{2} & 1 \ 0 & 0 & -1 & 1 \end{pmatrix}
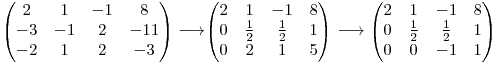
Pentru a obţine a doua matrice am înmulţit prima linie cu 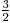\frac{3}{2} şi am adunat-o la a doua linie, iar apoi am adunat-o la ultima linie(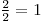\frac{2}{2}=1). Pentru a obţine ultima matrice am înmulţit a doua linie cu -\frac{2}{\frac{1}{2}}=-4.

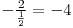Cum se poate observa şi din exemplu la fiecare pas construim o coloană şi o linie din matricea finală, coloana fiind umplută cu 0 sub linia fixată. Să presupunem că vrem să transformăm toate elementele de sub linia i aflate pe coloana j în 0. Pentru fiecare linie k ( k>i ) vom înmulţi linia i cu 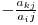-\frac{a_{kj}}{a_ij} şi o vom aduna la linia k astfel elementul de pe coloana j transformându-se în 0. În cazul în care 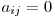a_{ij}=0 trebuie să căutăm o linie k(k > i) astfel încât 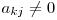a_{kj}\neq 0. În cazul în care această linie nu există, sistemul nu are soluţie. Aplicând aceşti pasi vom ajunge în final la o matrice triunghiulară din care vom afla necunoscutele.

Implementare

Codul de mai jos rezolva si cazul când avem mai multe ecuaţii decât necunoscute.

void elim(int n,int m,double s[][]) {//sistem cu n ecuatii m necunoscute
  for(int i=1,j=1,k;i<=n && j<=m;) {
    for(k=i;k<=n; ++k) 
      if(s[k][j]!=0) break;//cautam o linie pe care sa o folosim pentru a forma zerouri pe coloana j
    if(k>n) {//nu am gasit nicio linie pentru care s[i][j] e nenul deci trecem la urmatoarea coloana linia i nefiind finala
      ++j;
      continue;
    }
    if(k!=i)for(int l=1; l<=m+1; ++l) swap(s[i][l],s[k][l]);//interschimbam liniile pentru a avea pe linia i si coloana j un element nenul
    for(k=i+1; k<=n; ++k) 
      for(int l=m+1; l>=j; --l)
        s[k][l]-=((s[k][j]*s[i][l])/s[i][j]);//aplicam transformarea pentru fiecare linie mai mare ca i pentru a avea 0 pe coloana j sub linia i
    ++i; ++j;
  }
//aflam necunoscutele
  for(int i=n; i;--i) 
    for(int j=1; j<=m+1; ++j) if(fabs(s[i][j])>EPS) {
      //pentru ca e posibil sa avem mai multe ecuatii decat necunoscute
      //cautam pe fiecare linie primul coeficient nenul, acestia aparand de la dreapta la stanga
      if(j==m+1) {//linia nu are coeficienti nenuli deci nu avem solutie
        g<<"Imposibil";
        exit(0);
      }
      x[j]=s[i][m+1];
      for(int k=j+1; k<=m; ++k) x[j]-=s[i][k]*x[k];
      x[j]/=s[i][j];
      break;//trecem la linia precedenta
    }
}

Aplicaţii

The magic matrix
https://apps.topcoder.com/wiki/display/tc/TCO+2013+Round+2A#TheMagicMatrix
Go2
Gxor
Minesweeper

Bibliografie