Eliminare Gaussiană

(Categoria Algoritmi, Autor Petru Trîmbiţaş)

Descriere

Eliminarea Gaussiană este o metodă de rezolvare a ecuaţiilor matriciale de forma 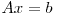Ax=b. Algoritmul nu este unul complicat, insă apare destul de des la concursurile de programare şi are aplicaţii interesante.

Să presupunem că avem următorul sistem:

\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{pmatrix} * \begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{pmatrix} = \begin{pmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{pmatrix}

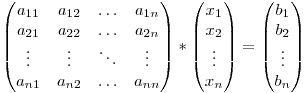
Pentru a rezolva sistemul vom transforma toate elementele de sub diagonala principală a matricei extinse în 0 pentru a putea scrie fiecare necunoscută doar în funcţie de necunoscutele cu indici mai mari.

\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} & b_{1}\\ a_{21} & a_{22} & \ldots & a_{2n} & b_{2}\\ a_{31} & a_{32} & \ldots & a_{3n} & b_{3}\\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} & b_{n} \end{pmatrix} \rightarrow \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} & b_{1}\\ 0 & a'_{22} & \ldots & a'_{2n} & b'_{2}\\ 0 & 0 & \ldots & a'_{3n} & b'_{3}\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & a'_{nn} & b'_{n} \end{pmatrix}

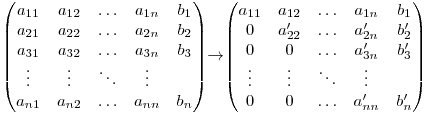
Având matricea sub această formă putem să aflăm uşor fiecare necunoscută din ecuaţia în care necunoscutele cu indici mai mici au coeficientul 0:
\: x_{n}=\frac{b'_{n}}{a'_{nn}}
x_{n-1}=\frac{b'_{n-1}-a'_{n-1n}*x_{n}}{a'_{n-1n-1}}
\vdots
x_{i}=\frac{b'_{i}-\sum\limits_{j=i+1}^n a'_{ij}*x_{j}}{a'_{ii}}

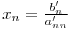
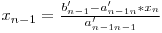
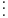
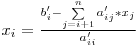
Acum că ştim să aflăm necunoscutele din forma triunghiulară a matricei ne mai rămâne doar să transformăm matricea.
Pentru a transforma matricea în formă triunghiulară vom aplica două operaţii:
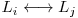L_{i} \longleftrightarrow L_{j} : interschimbarea a două linii
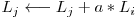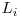L_{j} \longleftarrow L_{j}+a*L_{i} unde L_{i} este o linie a matricei extinse.

De exemplu:

\begin{pmatrix} 2 & 1 & -1 & 8 \ -3 & -1 & 2 & -11 \ -2 & 1 & 2 & -3 \end{pmatrix} \longrightarrow \begin{pmatrix} 2 & 1 & -1 & 8 \ 0 & \frac{1}{2} & \frac{1}{2} & 1 \ 0 & 2 & 1 & 5 \end{pmatrix} \longrightarrow \begin{pmatrix} 2 & 1 & -1 & 8 \ 0 & \frac{1}{2} & \frac{1}{2} & 1 \ 0 & 0 & -1 & 1 \end{pmatrix}
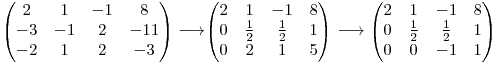
Pentru a obţine a doua matrice am înmulţit prima linie cu 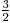\frac{3}{2} şi am adunat-o la a doua linie, iar apoi am adunat-o la ultima linie(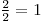\frac{2}{2}=1). Pentru a obţine ultima matrice am înmulţit a doua linie cu -\frac{2}{\frac{1}{2}}=-4.

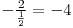Cum se poate observa şi din exemplu la fiecare pas construim o coloană şi o linie din matricea finală, coloana fiind umplută cu 0 sub linia fixată. Să presupunem că vrem să transformăm toate elementele de sub linia i aflate pe coloana j în 0. Pentru fiecare linie k ( k>i ) vom înmulţi linia i cu 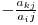-\frac{a_{kj}}{a_ij} şi o vom aduna la linia k astfel elementul de pe coloana j transformându-se în 0. În cazul în care 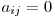a_{ij}=0 trebuie să căutăm o linie k(k > i) astfel încât 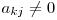a_{kj}\neq 0. În cazul în care această linie nu există, sistemul nu are soluţie. Aplicând aceşti pasi vom ajunge în final la o matrice triunghiulară din care vom afla necunoscutele. Complexitatea algoritmului este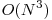 O(N^3)

Implementare

Codul de mai jos rezolva si cazul când avem mai multe ecuaţii decât necunoscute.

void elim(int n,int m,double s[][]) {//sistem cu n ecuatii m necunoscute
  for(int i=1,j=1,k;i<=n && j<=m;) {
    for(k=i;k<=n; ++k) 
      if(s[k][j]!=0) break;//cautam o linie pe care sa o folosim pentru a forma zerouri pe coloana j
    if(k>n) {//nu am gasit nicio linie pentru care s[i][j] e nenul deci trecem la urmatoarea coloana linia i nefiind finala
      ++j;
      continue;
    }
    if(k!=i)for(int l=1; l<=m+1; ++l) swap(s[i][l],s[k][l]);//interschimbam liniile pentru a avea pe linia i si coloana j un element nenul
    for(k=i+1; k<=n; ++k) 
      for(int l=m+1; l>=j; --l)
        s[k][l]-=((s[k][j]*s[i][l])/s[i][j]);//aplicam transformarea pentru fiecare linie mai mare ca i pentru a avea 0 pe coloana j sub linia i
    ++i; ++j;
  }
//aflam necunoscutele
  for(int i=n; i;--i) 
    for(int j=1; j<=m+1; ++j) if(fabs(s[i][j])>EPS) {
      //pentru ca e posibil sa avem mai multe ecuatii decat necunoscute
      //cautam pe fiecare linie primul coeficient nenul, acestia aparand de la dreapta la stanga
      if(j==m+1) {//linia nu are coeficienti nenuli deci nu avem solutie
        g<<"Imposibil";
        exit(0);
      }
      x[j]=s[i][m+1];
      for(int k=j+1; k<=m; ++k) x[j]-=s[i][k]*x[k];
      x[j]/=s[i][j];
      break;//trecem la linia precedenta
    }
}

Aplicaţii

Problema 1

Se dă un sistem cu variabile de tip boolean de forma celui de mai jos. Prin 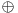\oplus am notat operatorul xor. Să se afle numărul de soluţii care verifică sistemul.
\begin{cases} x_{1} \oplus x_{2} \oplus x_{3} = 1 \ x_{1} \oplus x_{2} \oplus x_{4} = 1 \ x_{1} \oplus x_{3} \oplus x_{4} = 0 \ x_{2} \oplus x_{3} \oplus x_{4} = 1 \end{cases} \rightarrow \begin{pmatrix} 1 & 1 & 1 & 0 & 1 \ 1 & 1 & 0 & 1 & 1 \ 1 & 0 & 1 & 1 & 0 \ 0 & 1 & 1 & 1 & 1 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 1 & 1 & 0 & 1 \ 0 & 0 & 1 & 0 & 0 \ 0 & 1 & 0 & 1 & 1 \ 0 & 1 & 1 & 1 & 1 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 1 & 1 & 0 & 1 \ 0 & 1 & 0 & 1 & 1 \ 0 & 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 1 & 0 \end{pmatrix}

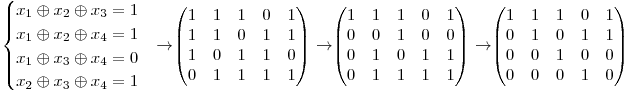
Soluţie

Această problemă este destul de des întâlnită la concursurile de programare şi pune unele dificultăţi deoarece toate variabilele depind între ele, problema neputând fi împărţită în subprobleme. Pentru a rezolva problema vom asocia sistemului o matrice în care pentru fiecare ecuaţie vom pune pe linia ei şi coloana corespunzătoare variabilelor care apar în ecuaţie valoarea 1, iar pe ultima coloană vom pune rezultatul ecuaţiei. Matricea obţinută vom încerca să o reducem. Pentru a o reduce vom folosi două operaţii:
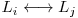L_{i} \longleftrightarrow L_{j} : interschimbarea a două linii
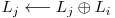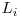L_{j} \longleftarrow L_{j} \oplus L_{i} unde L_{i} este o linie a matricei.
Având matricea redusă, numărul de soluţii este dat de numărul de coloane, fie el x, pe care nu am putut găsi un 1 cu care să reducem liniile de mai jos. Astfel celelalte variabile vor fi determinate în funcţie de variabila corespunzătoare acestei coloane, sistemul avand soluţie indiferent de valoarea variabilei. În final numărul de soluţii va fi 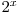2^x. Sistemul nu are soluţie atunci când avem o linie de forma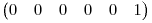 \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 1\end{pmatrix}

Go2 (Algoritmiada 2012 runda 4)

Problema ne cere să aflăm numărul de matrici de N x M ( N,M<101 ) binare cu unele celule deja completate astfel încât pentru orice căsuţă numărul de vecini(sus, jos, stânga, dreapta) care au valoarea 1 să fie par.

Soluţie

O primă soluţie ar fi să asociem fiecărei celule o variabilă, iar pentru fiecare celulă să scriem ecuaţia specifică: 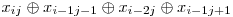x_{ij} \oplus x_{i-1j-1} \oplus x_{i-2j} \oplus x_{i-1j+1}. În final va rezulta un sistem cu MxN ecaţii şi MxN necunoscute. Complexitatea este 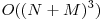O((N+M)^3) şi obţine 50 de puncte. Pentru a obţine 100 de puncte este necesar să observăm că dacă am fixat prima linie, a doua va fi unic determinată de ea. Aplicând acelaşi raţionament observăm că toata matricea poate fi calculată în funcţie de prima linie.
\begin{center} \begin{tabular}{| c | c | c | c |} \hline x_{1} & x_{2} & x_{3} & x_{4} \ \hline x_{2} & x_{1} \oplus x_{3} & x_{2} \oplus x_{4} & x_{3} \ \hline x_{1} \oplus x_{3} & x_{4} & x_{1} & x_{2} \oplus x_{4} \ \hline \end{tabular} \end{center}

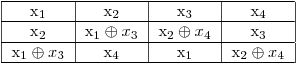
Astfel înlocuind variabilele cu cele corespunzătoare de pe prima linie rămânem cu un sistem cu M variabile şi MxN ecuaţii. În final complexitatea va fi 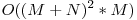O((M+N)^2*M)

Gxor (Campion 2011)

Se consideră o matrice cu N(N<30 001) linii şi N coloane (numerotate de la 1 la N). Fiecare element al matricei poate lua valoarea 0 sau 1. Se cunosc informaţii despre G(G<401) submatrice ale matricii considerate. A i-a submatrice este definită de parametrii l1(i), c1(i), l2(i) şi c2(i) (1≤l1(i)≤l2(i)≤N ; 1≤c1(i)≤c2(i)≤N). Se ştie că xor-ul tuturor elementelor din submatricea i (elementele cuprinse între liniile l1(i) şi l2(i) inclusiv şi între coloanele c1(i) şi c2(i) inclusiv) este x(i) (evident, x(i) este 0 sau 1).
Fie NM numărul de matrice binare cu N linii şi N coloane pentru care toate informaţiile despre cele G submatrice sunt adevărate (există în total 2N∙N matrici binare cu N linii şi N coloane, dar informaţiile despre cele G submatrice nu sunt neapărat adevărate pentru toate aceste matrice). Determinaţi restul împărţirii lui NM la 34949.

Soluţie

În mod evident o primă soluţie ar fi să considerăm fiecare celulă o necunoscută şi pentru fiecare informaţie să introducem o ecuaţie în sistem. Astfel vom avea N*N necunoscute, ceea ce este prea mult pentru a intra în timp. În continuare vom lucra cu matricea M[i][j] = suma xor a elementelor care se află în submatricea (1,1) (i,j), astfel pentru o informaţie x1, y1, x2, y2, r vom şti că M[x2][y2] xor M[x1-1][y2] xor M[x2][y1-1] xor M[x1-1][y1-1] = r. Vom aplica eliminarea gaussiană pe această matrice. Numărul de soluţii va fi 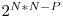2^{N*N-P}, unde P e numărul de variabile fixe din sistem.

XMAX (Spoj, sgu)

Se dă o mulţime de N (N<100 000) numere. Trebuie să aflăm submulţimea a cărei sumă xor este maximă.

Soluţie

Să presupunem că avem un număr şi dorim să aflăm dacă poate fi obţinut. Pentru asta vom construi un sistem în care fiecare ecuaţie corespunde unui bit, iar fiecare necunoscută corespunde unui număr dintre cele date. Dacă numărul are acel bit egal cu 1 atunci în ecuaţie va apărea pe poziţia numărului un 1(practic necunoscuta ne spune dacă considerăm acel număr în soluţie sau nu). Pentru fiecare bit din număr ecuaţia corespunzătoare va fi egală cu valoarea lui. Dacă sistemul are soluţie atunci există o submulţime a cărui xor să fie egal cu acel număr.

Acum ne rămâne să găsim numărul maxim pentru care sistemul are soluţie. Prima dată vom vedea dacă cel mai semnificativ bit poate fi egal cu 1. Pentru asta vom avea un sistem cu o singură ecuaţie corespunzătoare primului bit. Dacă are soluţie vom păstra ecuaţia şi vom încerca să setăm şi al doilea bit cu 1. În mod evident rezultatul va avea primul bit 1. Dacă nu, atunci vom păstra ecuaţia dar o vom egala cu 0. Pentru a afla soluţia vom adăuga pe rând câte o ecuaţie la sistem care iniţial va fi egală cu 1 iar dacă sistemul nu are soluţie o vom egala cu 0.

//v - şirul de numere
//DB numărul maxim de biţi din care poate fi format un număr
//ss - matricea extinsă
//sz - numărul de ecuaţii din sistem
for(int b=DB-1; b>=0; --b) for(int i=0; i<n; ++i) if(v[i]&(1LL<<b)) ss[DB-b-1][i]=1;
for(int b=DB-1; b>=0; --b) {
  ++sz;
  ss[sz-1][n]=1;
  if(areSolutie()) rez|=(1LL<<b);
  else ss[sz-1][n]=0;
}

XorCards
The magic matrix
https://apps.topcoder.com/wiki/display/tc/TCO+2013+Round+2A#TheMagicMatrix
Minesweeper
Cracking RSA
Find the operations

Bibliografie