Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2009-04-23 22:38:26.
Revizia anterioară   Revizia următoare  

Transformări geometrice

(Categoria Matematică, Autor Cosmin Negruşeri)

Introducere

În acest articol vom introduce câteva noţuni legate de transformările geometrice care se pot dovedi utile în concursurile de programare.

Înainte de toate prezentăm câteva aspecte teoretice, o mare parte din ele nefiind foarte interesante şi probabil sunt conţinute şi în manualele de liceu. Cititorul poate trece direct la probleme şi, în măsura în care noţiunile din soluţii îi sunt neclare, poate reveni asupra părţii teoretice.

Translaţia

Translaţia unei figuri geometrice reprezintă mişcarea tuturor componentelor ei pe o anumita distanţă si direcţie. Această transformare poate fi uşor caracterizată de un vector v = (dx, dy). Când vrem să translatăm un punct P(x, y) după v, e de ajuns să facem operaţia P’ = P + v. Astfel, P’ are cooronatele (x + dx, y + dy).

Proprietăţi:

  • păstrează distanţele;
  • pastrează orientarea poligoanelor (adică, dacă vârfurile poligonului sunt parcurse în ordine trigonometrică, atunci vârfurile corespondente din poligonul transformat vor fi şi ele în ordine trigonometrică);
  • păstrează unghiurile;
  • o dreaptă va fi transformată în altă dreaptă paralelă cu prima;
  • înafară de translaţia trivială de vector v = (0, 0), această transformare nu are puncte fixe (adică orice punct va fi transformat într-un punct diferit);
  • translaţii successive vor rezulta tot într-o translaţie (adică, dacă vrem să translatăm un punct dupa v şi apoi după v1, atunci obţinem acelaşi rezultat dacă translatăm direct după v + v1);
  • translaţia este comutativă;

Simetria

Există două tipuri de simetrii: simetria faţă de un punct şi simetria faţa de o dreaptă.

Un punct A îl are simetric pe A’ faţă de un punct O, dacă segmentul AA’ are ca mijloc punctul O. Dacă avem un punct (x0, y0) căruia vrem să îi aflăm simetricul faţă de un punct de coordonate (x, y) atunci acesta va fi (2x – x0, 2y – y0).

Proprietăţi:

  • păstrează distanţele;
  • păstrează orientarea poligoanelor (adică, dacă varfurile poligonului sunt parcurse în ordine trigonometrică, atunci vârfurile corespondente din poligonul transformat vor fi şi ele în ordine trigonometrică);
  • păstrează unghiurile;
  • drepte paralele vor fi transformate în drepte paralele;
  • are ca punct fix punctul O, iar drepte fixe cele care trec prin punctul O;
  • simetrii succesive după centre diferite O1(x1, y1) O2(x2, y2) sunt o translaţie de vector v = 2(x2 – x1);
  • simetriile după un punct nu comută;

Să calculăm simetricul unui punct P(x0, y0) faţă de o dreaptă de ecuaţie ax + by + c = 0. Notăm cu d distanţa de la punctul P la dreaptă, 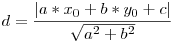d = \displaystyle\frac{|a*x_{0} + b*y_{0} + c|}{\sqrt{a^2 + b^2}} , şi cu (m1, m2) cosinii directori ai vectorului n(a, b) normal la dreaptă. Valorile cosinilor directori sunt: 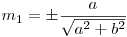m_{1} = \displaystyle \pm \frac{a}{\sqrt{a^2 + b^2}} şi m_{2} = \displaystyle \pm \frac{b}{\sqrt{a^2 + b^2}} . 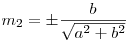Vom alege semnul minus dacă ax0 + by0 + c > 0 iar semnul plus dacă ax0 + by0 + c < 0. Astfel, simetricul punctului P va avea coordonatele (x0 + 2*d*m1, y0 + 2*d*m2).

Proprietăţi:

  • păstrează distanţele;
  • nu păstrează orientarea poligoanelor (adică, dacă varfurile poligonului sunt parcurse în ordine trigonometrică, atunci vârfurile corespondente din poligonul transformat vor fi în sens orar);
  • păstrează unghiurile;
  • drepte paralele vor fi transformate în drepte paralele;
  • are ca puncte fixe dreapta de simetrie;
  • simetrii succesive după drepte paralele sunt o translaţie;
  • simetrii succesive după drepte concurente sunt rotaţii;
  • simetriile nu comută;

Rotaţia

Aceasta este o transformare care roteşte punctele în sens trigonometric în jurul unui punct numit centru de rotaţie după un unghi fixat numit unghi de rotaţie. Dacă avem rotaţia de centru O(x0, y0) şi unghi alfa, atunci imaginea unui punct P(x, y) va fi P’(x0 + (x – x0) * cos(alfa) - (y – y0) * sin(alfa), y0 + (x – x0) * sin(alfa) + (y – y0) * cos(alfa)).

Proprietăţi:

  • păstrează distanţele;
  • păstrează orientarea poligoanelor;
  • păstrează unghiurile;
  • drepte paralele vor fi transformate în drepte paralele;
  • dacă nu este o rotaţie trivială de unghi 0 atunci are ca punct fix centrul de rotaţie;
  • nu are drepte fixe, dar are cercuri fixe centrate în centrul de rotaţie;
  • două rotaţii succesive R1(O1, alfa) şi R2(O2, beta) se compun într-o translaţie sau o rotaţie R3(O3, alfa + beta);
  • în general rotaţiile nu comută;

Omotetia

Aceasta este o transformare ce scalează obiectele în funcţie de un centru de omotetie şi un raport. Un punct P(x, y) transformat după o omotetie H(O(x0, y0), k) (centru O şi raport k) va avea imaginea P’(x0 + k * (x - x0), y0 + k * (y - y0)).

Proprietăţi:

  • nu păstrează distanţele;
  • păstrează orientarea poligoanelor;
  • păstrează unghiurile;
  • drepte paralele vor fi transformate în drepte paralele, iar transformata unei drepte va fi paralelă cu dreapta;
  • are ca punct fix centrul de omotetie;
  • două omotetii succesive H1(O1, k1) şi H2(O2, k2) se compun într-o translaţie sau omotetie H3(O3, k1 + k2);
  • în general omotetiile nu comută;

Desfăşurarea în plan

Aceasta nu este o transformare geometrică propriu-zisă, ci mai mult o tehnică folositoare în rezolvarea unor probleme pe care o puteţi vedea aplicată în problemele ce urmează ...

To do: de verificat teoria de aici. :)

Aplicaţia 1

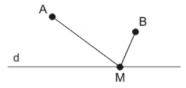
Fie două puncte A şi B de aceiaşi parte a unei drepte d. Se cere să se determine un punct M pe dreapta d cu proprietatea că suma AM + MB e mininimă.

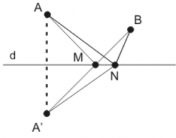
Rezolvare:

Ducem simetricul punctului A faţă de dreapta d pe care îl notăm cu A’. Oricare ar fi un punct N pe dreapta d, AN = A’N pentru că triunghiul AA’N este isoscel având dreapta d şi înălţime şi mediană. Astfel, avem că AN + NB = A’N + NB, deci pentru ca să minimizăm suma AM + MB trebuie de fapt să minimizăm suma A’M + MB. Punctele A’ şi B sunt situate de părţi diferite ale dreptei, deci punctul M trebuie situat la intersecţia segmentului A’B cu dreapta d.

Aplicaţia 2

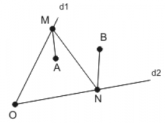
Fie două puncte A şi B în interiorul unui unghi format de semidreptele d1 şi d2 care au capătul comun O. Se cere să se determine două puncte M şi N astfel ca M să aparţină lui d1 şi N să aparţină lui d2 iar suma AM + MN + NB să fie minimă.

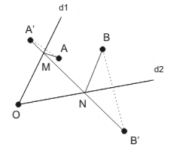
Rezolvare:

Folosim aceeaşi idee: ducem simetricul punctului A, notat cu A’, faţă de dreapta d1 şi simetricul punctului B notat cu B’ faţă de dreapta d2. Orice puncte M şi N am alege, avem că AM + MN + NB = A’M + MN + NB. Pentru a minimiza suma A’M + MN + NB’ trebuie ca M şi N să fie intersecţiile segmentului A’B’ cu semidreptele d1 şi d2.

Aplicaţia 3

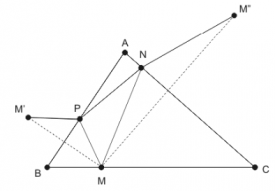
Dându-se un triunghi ascuţitunghic ABC se cere să se determine un triunghi înscris în acesta de perimetru minim.

Rezolvare:

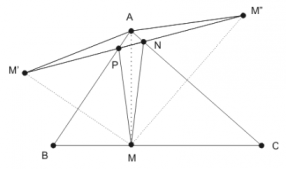
Luăm un punct M pe baza BC a triunghiului ABC, un punct P pe latura AB şi un punct N pe latura AC. Dacă avem M’ simetricul lui M faţă de AB şi M’’ simetricul lui M faţă de AC, atunci MN + NP + PM = M’’N + NP + PM’. Ca să minimizăm această sumă, punctele P şi N trebuie să fie la intersecţia segmentului M’M’’ cu laturile AB, respectiv AC. Perimetrul triunghiului MNP va fi egal cu lungimea segmentului M’M’’. Observăm că unghiul M’AM’’ are măsura egală cu 2 * măsura unghiului BAC şi că triunghiul M’AM’’ e isoscel de latură egală cu AM. Pentru ca M’M’’ să aibă lungimea minimă trebuie ca AM să fie cât mai scurt. Acest segment este minim atunci când M este piciorul înalţimii din A. La fel putem să deducem că N este piciorul înălţimii din B, iar P este piciorul înălţimii din C. Astfel, soluţia de perimetru minim este triunghiul ortic.

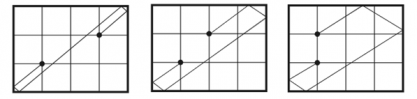
Aplicaţia 4: PolyLine (TopCoder)

Se consideră un dreptunghi cu colţurile de coordonate (0, 0) , (a, 0), (a, b), (0, b). Mai considerăm două puncte A şi B de coordonate (x1, y1) şi (x2, y2) în interiorul dreptunghiului. Se cere să se determine lungimea minimă a unei linii frânte ce porneşte din A ajunge în B şi intersectează fiecare latură a dreptunghiului. În figura de mai jos, avem un dreptunghi de dimensiuni 4 × 3 şi trei posibilităţi de a plasa două puncte în interiorul dreptunghiului, împreună cu soluţiile optime. Rezultatele pentru cele trei exemple sunt: 7.8102, 8.6023, respectiv 9.4339.

Rezolvare:

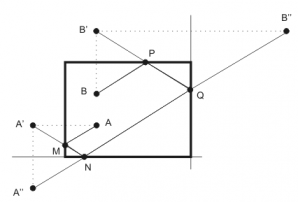
Este evident că o soluţie optimă va fi formată din cinci segmente. Putem încerca toate ordinele posibile ale drumului liniei frânte, fiind 4! = 24 asemenea ordini. Pentru fiecare ordine căutăm drumul optim. Acesta poate fi găsit folosind trucul prezentat în problemele anterioare. Să luăm un exemplu: pentru punctele A(1, 2) şi B(1,3) şi dreptunghiul de dimensiuni 4 şi 3, luăm punctele M, N, P, Q pe laturile din stânga, jos, dreapta respectiv sus ale dreptunghiului astfel încât să minimizăm suma AM + MN + NP + PQ + QB. Acum, vom duce simetricul lui A, notat cu A’, faţă de latura din stânga şi simetricul lui B, notat cu B’, faţă de latura de sus. Avem că AM = A’M şi QB = QB’. Deci, ca să minimizăm suma AM + MN + NP + PQ + QB trebuie să minimizăm suma A’M + MN + NP + PQ + QB’. Vom duce simetricul lui A’, notat prin A’’, faţă de latura de jos, şi simetricul lui B’, notat prin B’’, faţă de latura din dreapta. Avem că A’M + MN <= A’’N şi că PQ + QB’ <= QB’’, deci obţinem că pentru a minimiza suma AM + MN + NP + PQ + QB trebuie să minimizăm suma A’’M + MN + NB’’. Putem realiza acest obiectiv dacă M şi N vor fi intersecţiile segmentului A’’B’’ cu latura de jos, respectiv latura din dreapta a dreptunghiului, iar soluţia este exact distanţa de la A’’ la B’’.

Aplicaţia 5 (Olimpiada Letonă, 1997)

Laturile unui teren dreptunghiular de biliard de dimensiuni 43 × 73 sunt etichetate cu literele A, R, Z, D. O bilă B (dimensiunile căreia pot fi ignorate) este plasată în interiorul acestui teren la 13 centimetri distanţă de latura R şi la 29 de centimetri distanţă de latura D. Un jucător îşi pune tacul pe latura R la un punct ce e situat la K centimetri distanţă de latura D şi loveşte direct bila B. Bila se mişcă drept şi dacă e cazul loveşte marginile terenului. Mişcarea bilei se supune legilor fizicii, astfel, când bila se loveşte de margine ea va avea o traiectorie simetrică cu traiectoria iniţială faţă de dreapta perpendiculară pe margine în punctul de impact. O parte din traiectoria bilei o puteţi vedea în figură. Problema esta pentru un număr fix K (0 ≤ K ≤ 73) şi N (0 ≤ N ≤ 109). Să se determine distanţa bilei faţă de latura R şi distanţa faţă de latura D, după ce bila s-a deplasat exact N centimetri.

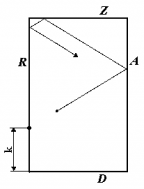
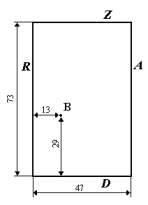
Rezolvare:

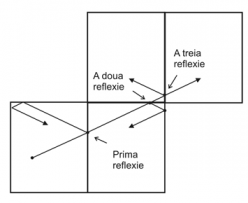
O rezolvare bazată pe simularea mişcării bilei pare anevoioasă, iar din cauza faptului că N poate fi foarte mare, acest algoritm nu este eficient. O rezolvare elegantă este următoarea. Întâi umplem planul cu o grilă infinită de dreptunghiuri de dimensiuni 43 × 73. Dacă am lăsa ca bila să îşi continue mişcarea şi am ignora prima lovire a marginii, în terenul adiacent, atunci traiectoria bilei ar fi de la trecerea marginii simetrică cu traiectoria normală a bilei, deci ar fi ca şi cum am reflecta întreaga tablă. Acest fenomen se repetă de fiecare dată când atingem o margine. Astfel, dacă ducem un segment pe direcţia de deplasare a bilei, ce pleacă din B, de lungime N, şi se termină în C atunci putem vedea în ce dreptunghi este el inclus, şi în funcţie de acest dreptunghi să transformăm punctul C în poziţia finală a bilei în dreptunghiul iniţial.