Transformări geometrice

(Categoria Matematică, Autor Cosmin Negruşeri)

• Conţinut:
• Introducere
  • Translaţia
  • Simetria
  • Rotaţia
  • Omotetia
  • Desfăşurarea în plan
• Aplicaţii
  • Aplicaţia 1
  • Aplicaţia 2
  • Aplicaţia 3
  • Aplicaţia 4: PolyLine (TopCoder)
  • Aplicaţia 5 (Olimpiada Letonă, 1997)
  • Aplicaţia 6: Pool (Timus)
  • Aplicaţia 7: NCushion (TopCoder)
  • Aplicaţia 8
  • Aplicaţia 9
  • Aplicaţia 10
  • Aplicaţia 11
  • Aplicaţia 12
  • Aplicaţia 13
  • Aplicaţia 14
  • Aplicaţia 15
  • Aplicaţia 16
  • Aplicaţia 17
  • Aplicaţia 18

Introducere

În acest articol vom introduce câteva noţuni legate de transformările geometrice care se pot dovedi utile în concursurile de programare.

Înainte de toate prezentăm câteva aspecte teoretice, o mare parte din ele nefiind foarte interesante şi probabil sunt conţinute şi în manualele de liceu. Cititorul poate trece direct la probleme şi, în măsura în care noţiunile din soluţii îi sunt neclare, poate reveni asupra părţii teoretice.

Translaţia

Translaţia unei figuri geometrice reprezintă mişcarea tuturor componentelor ei pe o anumita distanţă si direcţie. Această transformare poate fi uşor caracterizată de un vector v = (dx, dy). Când vrem să translatăm un punct P(x, y) după v, e de ajuns să facem operaţia P’ = P + v. Astfel, P’ are cooronatele (x + dx, y + dy).

Proprietăţi:

• păstrează distanţele;
• pastrează orientarea poligoanelor (adică, dacă vârfurile poligonului sunt parcurse în ordine trigonometrică, atunci vârfurile corespondente din poligonul transformat vor fi şi ele în ordine trigonometrică);
• păstrează unghiurile;
• o dreaptă va fi transformată în altă dreaptă paralelă cu prima;
• înafară de translaţia trivială de vector v = (0, 0), această transformare nu are puncte fixe (adică orice punct va fi transformat într-un punct diferit);
• translaţii successive vor rezulta tot într-o translaţie (adică, dacă vrem să translatăm un punct dupa v şi apoi după v₁, atunci obţinem acelaşi rezultat dacă translatăm direct după v + v₁);
• translaţia este comutativă;

Simetria

Există două tipuri de simetrii: simetria faţă de un punct şi simetria faţa de o dreaptă.

Un punct A îl are simetric pe A’ faţă de un punct O, dacă segmentul AA’ are ca mijloc punctul O. Dacă avem un punct (x₀, y₀) căruia vrem să îi aflăm simetricul faţă de un punct de coordonate (x, y) atunci acesta va fi (2x – x₀, 2y – y₀).

Proprietăţi:

• păstrează distanţele;
• păstrează orientarea poligoanelor (adică, dacă varfurile poligonului sunt parcurse în ordine trigonometrică, atunci vârfurile corespondente din poligonul transformat vor fi şi ele în ordine trigonometrică);
• păstrează unghiurile;
• drepte paralele vor fi transformate în drepte paralele;
• are ca punct fix punctul O, iar drepte fixe cele care trec prin punctul O;
• simetrii succesive după centre diferite O₁(x₁, y₁) O₂(x₂, y₂) sunt o translaţie de vector v = 2(x₂ – x₁);
• simetriile după un punct nu comută;

Să calculăm simetricul unui punct P(x₀, y₀) faţă de o dreaptă de ecuaţie ax + by + c = 0. Notăm cu d distanţa de la punctul P la dreaptă, 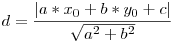, şi cu (m₁, m₂) cosinii directori ai vectorului n(a, b) normal la dreaptă. Valorile cosinilor directori sunt: 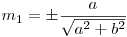şi 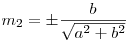. Vom alege semnul minus dacă ax₀ + by₀ + c > 0 iar semnul plus dacă ax₀ + by₀ + c < 0. Astfel, simetricul punctului P va avea coordonatele (x₀ + 2*d*m₁, y₀ + 2*d*m₂).

Proprietăţi:

• păstrează distanţele;
• nu păstrează orientarea poligoanelor (adică, dacă varfurile poligonului sunt parcurse în ordine trigonometrică, atunci vârfurile corespondente din poligonul transformat vor fi în sens orar);
• păstrează unghiurile;
• drepte paralele vor fi transformate în drepte paralele;
• are ca puncte fixe dreapta de simetrie;
• simetrii succesive după drepte paralele sunt o translaţie;
• simetrii succesive după drepte concurente sunt rotaţii;
• simetriile nu comută;

Rotaţia

Aceasta este o transformare care roteşte punctele în sens trigonometric în jurul unui punct numit centru de rotaţie după un unghi fixat numit unghi de rotaţie. Dacă avem rotaţia de centru O(x₀, y₀) şi unghi alfa, atunci imaginea unui punct P(x, y) va fi P’(x₀ + (x – x₀) * cos(alfa) - (y – y₀) * sin(alfa), y₀ + (x – x₀) * sin(alfa) + (y – y₀) * cos(alfa)).

Proprietăţi:

• păstrează distanţele;
• păstrează orientarea poligoanelor;
• păstrează unghiurile;
• drepte paralele vor fi transformate în drepte paralele;
• dacă nu este o rotaţie trivială de unghi 0 atunci are ca punct fix centrul de rotaţie;
• nu are drepte fixe, dar are cercuri fixe centrate în centrul de rotaţie;
• două rotaţii succesive R₁(O₁, alfa) şi R₂(O₂, beta) se compun într-o translaţie sau o rotaţie R₃(O₃, alfa + beta);
• în general rotaţiile nu comută;

Omotetia

Aceasta este o transformare ce scalează obiectele în funcţie de un centru de omotetie şi un raport. Un punct P(x, y) transformat după o omotetie H(O(x₀, y₀), k) (centru O şi raport k) va avea imaginea P’(x₀ + k * (x - x₀), y₀ + k * (y - y₀)).

Proprietăţi:

• nu păstrează distanţele;
• păstrează orientarea poligoanelor;
• păstrează unghiurile;
• drepte paralele vor fi transformate în drepte paralele, iar transformata unei drepte va fi paralelă cu dreapta;
• are ca punct fix centrul de omotetie;
• două omotetii succesive H₁(O₁, k₁) şi H₂(O₂, k₂) se compun într-o translaţie sau omotetie H₃(O₃, k₁ + k₂);
• în general omotetiile nu comută;

Desfăşurarea în plan

Aceasta nu este o transformare geometrică propriu-zisă, ci mai mult o tehnică folositoare în rezolvarea unor probleme pe care o puteţi vedea aplicată în problemele ce urmează ...

To do: de verificat teoria de aici. :)

Aplicaţia 1

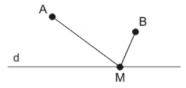
Fie două puncte A şi B de aceiaşi parte a unei drepte d. Se cere să se determine un punct M pe dreapta d cu proprietatea că suma AM + MB e mininimă.

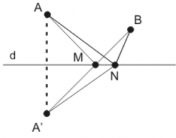
Rezolvare:

Ducem simetricul punctului A faţă de dreapta d pe care îl notăm cu A’. Oricare ar fi un punct N pe dreapta d, AN = A’N pentru că triunghiul AA’N este isoscel având dreapta d şi înălţime şi mediană. Astfel, avem că AN + NB = A’N + NB, deci pentru ca să minimizăm suma AM + MB trebuie de fapt să minimizăm suma A’M + MB. Punctele A’ şi B sunt situate de părţi diferite ale dreptei, deci punctul M trebuie situat la intersecţia segmentului A’B cu dreapta d.

Aplicaţia 2

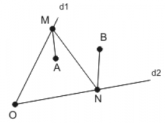
Fie două puncte A şi B în interiorul unui unghi format de semidreptele d₁ şi d₂ care au capătul comun O. Se cere să se determine două puncte M şi N astfel ca M să aparţină lui d₁ şi N să aparţină lui d₂ iar suma AM + MN + NB să fie minimă.

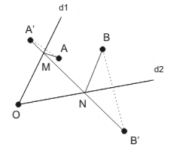
Rezolvare:

Folosim aceeaşi idee: ducem simetricul punctului A, notat cu A’, faţă de dreapta d₁ şi simetricul punctului B notat cu B’ faţă de dreapta d₂. Orice puncte M şi N am alege, avem că AM + MN + NB = A’M + MN + NB’. Pentru a minimiza suma A’M + MN + NB’ trebuie ca M şi N să fie intersecţiile segmentului A’B’ cu semidreptele d₁ şi d₂.

Aplicaţia 3

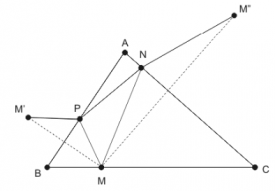
Dându-se un triunghi ascuţitunghic ABC se cere să se determine un triunghi înscris în acesta de perimetru minim.

Rezolvare:

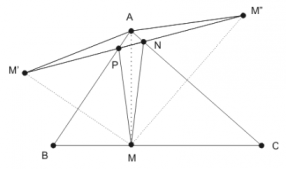
Luăm un punct M pe baza BC a triunghiului ABC, un punct P pe latura AB şi un punct N pe latura AC. Dacă avem M’ simetricul lui M faţă de AB şi M’’ simetricul lui M faţă de AC, atunci MN + NP + PM = M’’N + NP + PM’. Ca să minimizăm această sumă, punctele P şi N trebuie să fie la intersecţia segmentului M’M’’ cu laturile AB, respectiv AC. Perimetrul triunghiului MNP va fi egal cu lungimea segmentului M’M’’. Observăm că unghiul M’AM’’ are măsura egală cu 2 * măsura unghiului BAC şi că triunghiul M’AM’’ e isoscel de latură egală cu AM. Pentru ca M’M’’ să aibă lungimea minimă trebuie ca AM să fie cât mai scurt. Acest segment este minim atunci când M este piciorul înalţimii din A. La fel putem să deducem că N este piciorul înălţimii din B, iar P este piciorul înălţimii din C. Astfel, soluţia de perimetru minim este triunghiul ortic.

Aplicaţia 4: PolyLine (TopCoder) X

Se consideră un dreptunghi cu colţurile de coordonate (0, 0) , (a, 0), (a, b), (0, b). Mai considerăm două puncte A şi B de coordonate (x₁, y₁) şi (x₂, y₂) în interiorul dreptunghiului. Se cere să se determine lungimea minimă a unei linii frânte ce porneşte din A ajunge în B şi intersectează fiecare latură a dreptunghiului. În figura de mai jos, avem un dreptunghi de dimensiuni 4 × 3 şi trei posibilităţi de a plasa două puncte în interiorul dreptunghiului, împreună cu soluţiile optime. Rezultatele pentru cele trei exemple sunt: 7.8102, 8.6023, respectiv 9.4339.

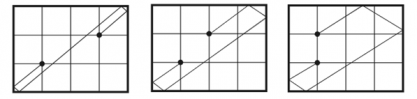
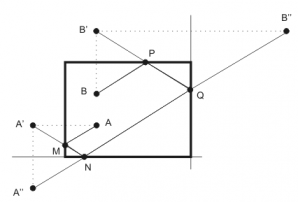
Rezolvare:

Este evident că o soluţie optimă va fi formată din cinci segmente. Putem încerca toate ordinele posibile ale drumului liniei frânte, fiind 4! = 24 asemenea ordini. Pentru fiecare ordine căutăm drumul optim. Acesta poate fi găsit folosind trucul prezentat în problemele anterioare. Să luăm un exemplu: pentru punctele A(1, 2) şi B(1,3) şi dreptunghiul de dimensiuni 4 şi 3, luăm punctele M, N, P, Q pe laturile din stânga, jos, dreapta respectiv sus ale dreptunghiului astfel încât să minimizăm suma AM + MN + NP + PQ + QB. Acum, vom duce simetricul lui A, notat cu A’, faţă de latura din stânga şi simetricul lui B, notat cu B’, faţă de latura de sus. Avem că AM = A’M şi QB = QB’. Deci, ca să minimizăm suma AM + MN + NP + PQ + QB trebuie să minimizăm suma A’M + MN + NP + PQ + QB’. Vom duce simetricul lui A’, notat prin A’’, faţă de latura de jos, şi simetricul lui B’, notat prin B’’, faţă de latura din dreapta. Avem că A’M + MN <= A’’N şi că PQ + QB’ <= QB’’, deci obţinem că pentru a minimiza suma AM + MN + NP + PQ + QB trebuie să minimizăm suma A’’M + MN + NB’’. Putem realiza acest obiectiv dacă M şi N vor fi intersecţiile segmentului A’’B’’ cu latura de jos, respectiv latura din dreapta a dreptunghiului, iar soluţia este exact distanţa de la A’’ la B’’.

Aplicaţia 5 (Olimpiada Letonă, 1997)

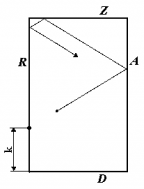
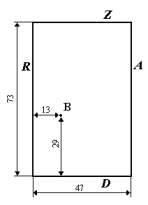
Laturile unui teren dreptunghiular de biliard de dimensiuni 43 × 73 sunt etichetate cu literele A, R, Z, D. O bilă B (dimensiunile căreia pot fi ignorate) este plasată în interiorul acestui teren la 13 centimetri distanţă de latura R şi la 29 de centimetri distanţă de latura D. Un jucător îşi pune tacul pe latura R la un punct ce e situat la K centimetri distanţă de latura D şi loveşte direct bila B. Bila se mişcă drept şi dacă e cazul loveşte marginile terenului. Mişcarea bilei se supune legilor fizicii, astfel, când bila se loveşte de margine ea va avea o traiectorie simetrică cu traiectoria iniţială faţă de dreapta perpendiculară pe margine în punctul de impact. O parte din traiectoria bilei o puteţi vedea în figură. Problema esta pentru un număr fix K (0 ≤ K ≤ 73) şi N (0 ≤ N ≤ 10⁹). Să se determine distanţa bilei faţă de latura R şi distanţa faţă de latura D, după ce bila s-a deplasat exact N centimetri.

Rezolvare:

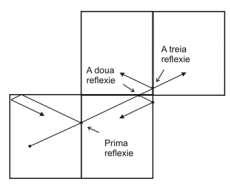
O rezolvare bazată pe simularea mişcării bilei pare anevoioasă, iar din cauza faptului că N poate fi foarte mare, acest algoritm nu este eficient. O rezolvare elegantă este următoarea. Întâi umplem planul cu o grilă infinită de dreptunghiuri de dimensiuni 43 × 73. Dacă am lăsa ca bila să îşi continue mişcarea şi am ignora prima lovire a marginii, în terenul adiacent, atunci traiectoria bilei ar fi de la trecerea marginii simetrică cu traiectoria normală a bilei, deci ar fi ca şi cum am reflecta întreaga tablă. Acest fenomen se repetă de fiecare dată când atingem o margine. Astfel, dacă ducem un segment pe direcţia de deplasare a bilei, ce pleacă din B, de lungime N, şi se termină în C atunci putem vedea în ce dreptunghi este el inclus, şi în funcţie de acest dreptunghi să transformăm punctul C în poziţia finală a bilei în dreptunghiul iniţial.

Aplicaţia 6: Pool (Timus)

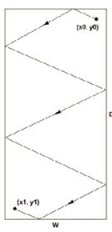
Programatorului Vasile îi place să se plimbe prin biroul lui dreptunghiular. El începe drumul din locul unde este situat biroul lui şi se plimbă până când crede că ar trebui să se apuce de lucru din nou. Drumul lui urmează legea de mişcare dată de „unghiul de incidenţă este egal cu unghiul de reflexie”. Vasile se mişcă de la zid la zid în linie dreaptă. Şeful direct al lui Vasile este interesat cât timp pierde acesta în plimbările lui. Este uşor să aflăm timpul, împărţind distanţa parcursă la viteza medie a lui Vasile (aceasta a fost deja calculată de şef), deci trebuie să se afle distanţa parcursă. Se ştie ordinea în care au fost atinşi pereţii întrucât Vasile, fiind neatent, se loveşte de pereţi şi astfel se aud bufniturile în fiecare zid. Se dau dimensiunile camerei lui Vasile: W şi D (0 ≤ W, D ≤ 100), poziţia iniţială, poziţia finală şi secvenţa de litere N, S, E, V care este ordinea în care sunt atinşi pereţii. De exemplu, în imagine pereţii sunt atinşi în ordinea NVEVES. Numărul de coliziuni nu depăşeste 1000, poziţiile iniţiale şi finale nu se află pe marginile dreptunghiului, iar drumul lui Vasile nu va trece prin vreun colţ al încăperii.

Rezolvare:

Precum în problema anterioară, când Vasile atinge un perete mişcarea lui se oglindeşte faţă de mişcarea normală. Vom procesa fiecare instrucţiune din şirul în care e prezentată ordinea atingerii pereţilor. O instrucţiune va însemna o reflexie a dreptunghiului curent şi a punctului destinaţie al lui Vasile. După ce vom procesa toate coliziunile obţinem dreptunghiul final şi punctul de destinaţie transformat în interiorul acestui dreptunghi. Acum linia frântă care unea punctul de start s-a transformat într-un segment de dreaptă între punctul de start şi imaginea punctului final după ce s-a realizat asupra lui seria de transformări.

Aplicaţia 7: NCushion (TopCoder)

Pe o masă de biliard de dimensiuni 2000 × 1000 sunt aşezate două bile la coordonate întregi. Se cere să se determine numărul de posibilităţi de lovire a primei bile, astfel ca ea să lovească exact de N ori manta (1 ≤ N ≤ 500) şi apoi să lovească cea de a doua bilă. Mişcarea bilei se consideră ideală, iar dacă bila loveşte un colţ se consideră că s-au atins două mante şi bila se va mişca pe aceiaşi direcţie în sens opus.

Rezolvare:

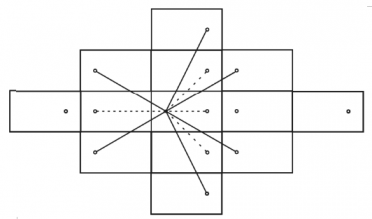
Soluţia foloseşte ideea de mai sus de a reflecta tabla de biliard împreună cu poziţia celei de a doua bile. Aşa cum am văzut în problema anterioară, fiecare şir de atingeri al mantelor ne dă exact un mod în care prima bilă o poate lovi pe cea de a doua. Dacă ştim în ce dreptunghi reflectat vrem să lovim bila a doua, fixând acest dreptunghi, avem o direcţie fixată şi un şir de mante fix pe care le va atinge bila dacă va fi lovită în acea direcţie. În figură avem cazul în care trebuie să lovim exact două mante înainte să atingem a doua bilă.

În desen am colorat cu negru bila iniţială şi cu alb a doua bilă şi imaginile ei. Cu linie punctată am desenat traiectoriile care ar fi atins bila a doua fără a atinge de două ori manta şi cu linie neagră direcţiile pe care manta ar fi atinsă exact de două ori. Observăm că pentru a atinge manta de N ori o bilă trebuie să intre în N alte dreptunghiuri. Deci, asociem poziţiilor dreptunghiurilor un sistem de coordonate în care dreptunghiul iniţial are coordonatele (0, 0). Pentru ca bila să atingă exact N mante, coordonatele (x, y) ale dreptunghiului trebuie să satisfacă egalitatea |x| + |y| = N. Mai trebuie să avem grijă ca drumul bilei care atinge N mante să nu atingă a doua bilă înainte de atingerea tuturor mantelor. Aceste observaţii ne duc la următoarea soluţie: pentru toate dreptunghiurile (x, y), care satisfac proprietatea |x| + |y| < N, păstrăm într-o structură de date (structura preferată de autor ar fi un tabel de dispersie) vectorul asociat direcţiei pe care ar fi trebuit lovită prima bilă pentru a ajunge la imaginea celei de a doua bile din acest dreptunghi. Apoi, pentru fiecare dreptunghi pentru care |x| + |y| = N, dacă direcţia asociată lui nu este în structura de date, incrementăm numărul de soluţii. Această rezolvare are complexitatea O(N² log N) pentru că normalizarea unei direcţii implică folosirea algoritmului lui Euclid ce are complexitate O(log N).

Aplicaţia 8: PuckShot (TopCoder)

Un jucător de hockey stângaci are o mişcare în care de la mijlocul terenului izbeşte pucul de marginea terenului care apoi întră în spaţiul porţii. Terenul este de 3000 de centimetri lăţime. Distanţa între linia de mijloc şi linia de gol este de 1733 de centimetri. Poarta este centrată pe linia de gol şi are dimensiunea de 183 de centimetri. Când jucătorul loveşte, puc-ul se va lovi de marginea terenului şi apoi va ricoşa simetric în poartă. Pucul şi stâlpii porţii vor fi considerate puncte. Pe gheaţă vor fi cel mult nouă jucători care vor fi modelaţi ca segmente orizontale de lungime 50 centimetri. Pentru ca lovitura să aibă succes, traiectoria ei nu trebuie să intersecteze niciun jucător. Pentru simplitate, puteţi presupune că terenul este perfect dreptunghiular. Se cere unghiul format de lovitura jucătorului cu linia de mijloc, astfel ca lovitura să fie cu succes şi pucul să intre în poartă şi să fie cât mai apropiat de stâlpul drept al porţii. Structura unui teren de hockey este prezentată în următoarea figură:

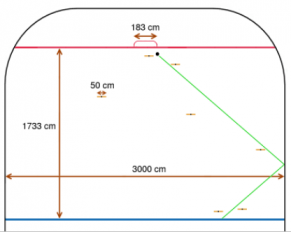
Rezolvare:

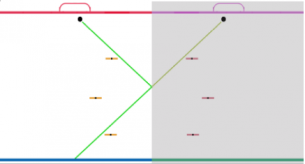
O rezolvare posibilă ar fi să pornim cu o lovitură de un unghi fixat şi să vedem dacă ajunge în poartă, iar apoi să creştem unghiul loviturii puţin câte puţin. Prin folosirea unor consideraţii de simetrie putem rezolva problema mai uşor şi mai eficient. Oglindim terenul împreună cu toţi jucătorii. Astfel, transformăm lovitura din două segmente în unul singur care trece prin dreapta de simetrie. Acum, luăm fiecare punct lateral al jucătorilor, fiecare punct lateral al imaginii reflectate ale jucătorilor şi punctele porţii reflectate, şi unim aceste puncte cu punctul de unde jucătorul va lovi pucul. Verificăm care dintre aceste drepte dacă sunt rotite foarte puţin la dreapta sau la stânga intersectează imaginea porţii reflectate şi nu intersectează segmentele ce reprezintă jucătorii sau imaginea lor reflectată. Astfel, soluţia noastră are complexitatea O(N²) unde N este numărul de jucători, pentru că pentru fiecare dintre cele 4N + 2 raze trebuie să verificăm intersecţia cu 2N + 1 segmente. Pe acestă idee putem realiza o soluţie în O(N log N) folosind o linie de baleiere care trece prin punctul iniţial si se mişcă circular în jurul lui.

Aplicaţia 9: Poligon 2 (infoarena)

Se dau coordonatele mijloacelor laturilor unui poligon nu neapărat convex şi care se poate autointersecta. Se cere să se determine coordonatele vârfurilor poligonului.

Rezolvare:

Considerăm că poligonul are N vârfuri. Rezolvăm problema întâi pentru N par. Luăm primul vârf al poligonului, şi îi determinăm simetricul faţă de primul mijloc de latură. Astfel găsim al doilea vârf. Dacă luăm al doilea vârf printr-o simetrie îl obţinem pe al treilea ş.a.m.d. Deci prin N simetrii obţinem din nou primul punct. Cum N este par fiecare două simetrii compuse sunt o translaţie, deci avem o serie de translaţii care se compun într-una care duce punctul iniţial în punctul iniţial. Aşa cum am vazut la partea teoretică translaţia are un punct fix doar dacă ea e translaţie trivială. Translaţia fiind trivială, putem porni cu orice punct din plan şi să obţinem celelalte N + 1 puncte din poligon ca şi rezultate ale simetriilor aplicate succesiv. În cazul în care N e impar transformarea explicată mai sus are ca rezultat compunerea între o translaţie şi o simetrie, compunere care aşa cum puteţi verifica are ca rezultat o simetrie de alt centru. Dar punctul iniţial este transformat în acelaşi punct, deci el trebuie să fie centrul de simetrie al transformării compuse. şi, atunci luăm un punct oarecare P în plan, efectuăm cele N transformări asupra lui şi obţinem un punct P’. Primul punct al poligonului va fi mijlocul acestui segment.

Aplicaţia 10: Dmg (Stelele Informaticii 2005, infoarena)

Se dau N (1 ≤ N ≤ 1500) puncte de coordonate întregi. Să se determine numărul de axe de simetrie al sistemului de puncte.

Rezolvare:

Axele de simetrie ale sistemului de puncte trebuie să fie şi axe de simetrie pentru poligonul ce reprezintă înfăşurătoarea convexă a acestor puncte. Dacă vrem să găsim axele de simetrie ale unui poligon convex, observăm că dacă el are număr par de vârfuri, atunci trebuie ca acestea sau să fie mediatoare pentru o latură a poligonului, sau să treacă prin două vârfuri. Dacă el are număr impar de laturi atunci axele de simetrie trebuie să fie mediatoare pentru o latură şi să treacă printr-un punct al poligonului. Astfel, după calcularea în O(N log N) a înfăţurătorii convexe, putem afla în timp O(N) care sunt candidate la axa de simetrie a poligonului. Verificarea faptului dacă o dreaptă este axă de simetrie pentru un set de puncte o putem face în O(N) folosindu-ne de o tabelă de dispersie. Algoritmul de determinare a axelor de simetrie are complexitatea finală O(N²).

Aplicaţia 11 (ONM 1997, clasa a VIII-a)

Se dă un paralelipiped ABCDEFGH, cu AB = 5, BC = 4, AE = 3. Se cere să determinăm poziţia unui punct M ce aparţine segmentului BF cu proprietatea că suma AM + MG este minimă.

Rezolvare

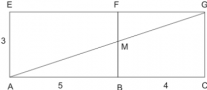
Pentru această problemă ne putem imagina o soluţie analitică în care vrem să minimizăm funcţia AM + MG care depinde de coordonata y, dar o asemenea rezolvare nu ar fi fost accesibilă unui elev de clasa a VIII-a. O soluţie elegantă şi simplă este următoarea. Desfăşurăm în plan feţele ABFE şi BCGD. Astfel se formează dreptunghiul ACGE, unde AC = 9 şi AE = 3. Acum este clar că punctul M trebuie să fie intersecţia diagonalei AG cu FB. De aici putem găsi foarte uşor că BM = 5/3.

Aplicaţia 12 (TopCoder)

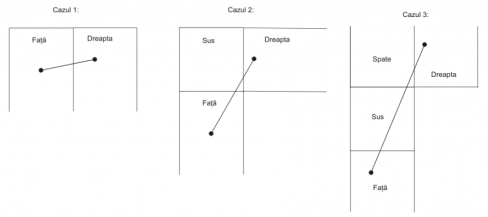
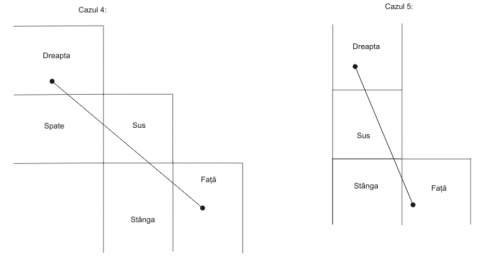
Pe partea frontală a unui zgârie-nor foarte înalt, ce are forma unui paralelipiped, cu baza un pătrat de latura 200 de metri, este situat un păianjen. Acesta vrea să mănânce o muscă situată pe faţa din dreapta a zgârie-norului. ştiind coordonatele păianjenului şi ale muştei vi se cere să determinaţi drumul cel mai scurt pe care îl poate face păianjenul ca să mănânce musca iar întreaga deplasare a lui să fie pe suprafaţa zgârie-norului (coordonatele gângăniilor se măsoară relativ la colţul stânga sus al feţei pe care se află fiecare).

Rezolvare:

Desfăşurăm paralelipipedul în toate modurile posibile (aşa cum vedem în figură) şi alegem dintre toate drumurile soluţia optimă.

Aplicaţia 13

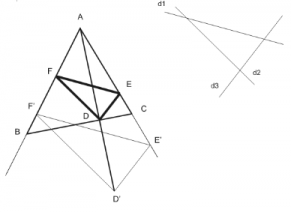
Se dă un triunghi ABC şi trei drepte d₁, d₂ şi d₃ care nu sunt paralele între ele două câte două. Se cere să se determine un triunghi înscris în triunghiul ABC ce are laturile paralele cu dreptele d₁, d₂ respectiv d₃.

Rezolvare:

Construim un triunghi D’E’F’ ce are laturile paralele cu dreptele d₁, d₂ şi d₃, iar punctul E’ aparţine semidreptei [AC şi punctul F’ aparţine semidreptei [AB. Acum fixăm un punct D în intersecţia lui AD’ cu BC şi în acest punct ducem două drepte paralele cu dreptele d₁ şi d₂. Aceste drepte vor intersecta laturile triunghiului în punctele F şi E. În omotetia de centru A şi raport AD / AD’ triunghiul D’E’F’ se transformă în DEF, care este un triunghi ce respectă condiţia din enunţ.

Aplicaţia 14: Triangular Square (UVa)

Se dă un triunghi ABC. Vrem să găsim aria maximă a unui pătrat situat în întregime în interiorul triunghiului. În imagine avem un pătrat în interiorul unui triunghi, dar acesta nu este de arie maximă. De exemplu într-un triunghi cu laturile de dimensiuni 6, 6 şi 6, aria maximă este 7.754051.

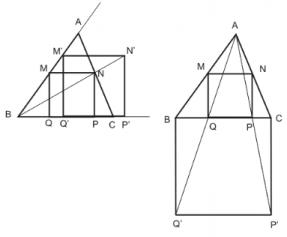
Rezolvare:

Pornim de la presupunerea intuitivă că cel mai mare pătrat ce se poate plasa în interiorul unui triunghi trebuie să aibă una din laturi pe o latură a triunghiului. Astfel, pentru a determina pătratul de arie maximă avem trei posibilităţi de aşezare pe laturile triunghiului. Pentru o aşezare fixată putem afla uşor pătratul maxim din interiorul triunghiului ce are două varfuri pe latura BC. O modalitate ar fi să desenăm un pătrat M’N’P’Q’ ce are punctele Q’ şi P’ pe semidreapta [BC şi punctul M’ pe semidreapta [BA. După care, luăm punctul N ca intersecţie a dreptei BN’ cu AC. Găsim pătratul MNPQ ca fiind omoteticul pătratului M’N’P’Q’ după omotetia de centru B şi raport BN / BN’. Altă modalitate de construcţie a pătratului ar fi cea prezentată în a doua figură, adică: se construieşte în exterior, pe latura BC a triunghiului, un pătrat BCQ’P’, se determină punctele P şi Q ca şi intersecţii al segmentului AQ’ cu BC şi al segmentului AP’ cu BC. Pătratul MNPQ va fi omoteticul pătratului BCP’Q’, după omotetia de centru A şi raport QP / BC.

Aplicaţia 15: Arhipelago (SGU)

Se dau coordonatele a două vârfuri ale unui poligon regulat de N laturi. Se cere, dacă ştiţi pe N, cele două perechi de coordonate şi N₁, N₂ indicii celor două puncte pe poligon, să determinaţi coordonatele tuturor celor N vârfuri.

Rezolvare:

Fie O centrul cercului circumscris poligonului regulat. Dacă notăm A şi B cele două puncte, atunci putem uşor să determinăm măsura unghiului AOB pe care o notăm cu alfa. Triunghiul AOB este isoscel şi ştim că are la bază unghiuri de măsură beta = (180 – alfa) / 2. Pentru a determina punctul O vom roti dreapta AB în jurul lui A după un unghi beta, şi vom roti dreapta AB în jurul lui B după un unghi beta. Cele două drepte ce rezultă din cele două rotaţii se vor intersecta în punctul O. Astfel, am găsit centrul cercului circumscris poligonului, pentru a găsi punctele lui îi aplicăm vârfului A rotaţiile de centru O şi unghiuri 360K/N unde K ia toate valorile naturale de la 1 la N.

Aplicaţia 16: Geometrical dreams (Timus)

Pe laturile unui poligon A₁A₂...A_N (vârfurile A_i sunt numerotate în ordine trigonometrică), se construiesc în exterior triunghiurile isoscele A_iM_iA_i+1, iar unghiul A_iM_iA_i+1 = alfa_i (aici A_N+1 = A₁). Suma măsurilor unghiurilor alfa_i nu este multiplu de 360 de grade. Dacă ni se dau N ≤ 50, coordonatele punctelor M_i şi unghiurile alfa_i, scrieţi un program care ne dă coordonatele vârfurilor poligonului.

Rezolvare:

Aşa cum am văzut în partea teoretică, o compunere de mai multe rotaţii are ca rezultat o rotaţie al cărei unghi este suma unghiurilor rotaţiilor parţiale. Dacă pornim cu punctul A₁ şi îl rotim în jurul lui M₁ cu un unghi alfa₁, după care luăm punctul rezultat şi îl rotim în jurul lui M₂ cu unghiul alfa₂ şi aşa mai departe până când am rotit pe A₁ în punctelor M₁, M₂, ... M_n. Efectuând aceşti paşi vom obţine pe rând vârfurile poligonului, iar la sfârşit A₁ va ajunge din nou în poziţia iniţială. Acest procedeu este de fapt o serie de rotaţii, şi vedem că aplicarea lui asupra lui A₁ îl lasă neschimbat. Cum suma măsurilor unghiurilor de rotaţie nu este multiplu de 360 de grade, înseamnă că rotaţia nu este trivială, iar o rotaţie netrivială are ca punct fix doar centrul ei. Aşadar putem lua un punct oarecare în plan asupra căruia aplicăm procedeul şi vom obţine imaginea lui. Folosind aceste două puncte şi alfa = suma de alfa_i ca unghi de rotaţie, putem determina centrul A₁ de rotaţie. După care efectuând transformările asupra lui A₁ obţinem celelalte puncte ale poligonului.

Aplicaţia 17: Texan (Baraj ONI, 2005)

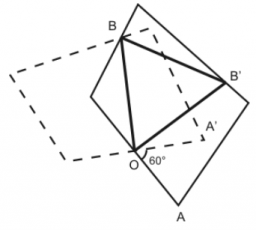
Se dă un poligon convex de N vârfuri (3 ≤ N ≤ 700). Se cere să se determine un triunghi echilateral cu vârfurile aparţinând laturilor poligonului convex.

Rezolvare:

Luăm un punct O pe o latură a poligonului. Rotim întreg poligonul în jurul acestui punct 60 de grade în sens trigonometric. Poligonul rotit va intersecta poligonul iniţial într-un nou punct B. Acest punct B îl rotim în jurul lui O cu 60 de grade în sens orar. Rezultatul este un punct B’ care evident aparţine poligonului iniţial. Acum triunghiul OBB’ este echilateral pentru că OB = OB’ şi măsura unghiului BOB’ este de 60 de grade. Menţionăm că aceasta a fost una dintre cele mai dure probleme de la selecţia lotului de anul acesta. O rezolvare de complexitate O(N²) a fost de ajuns pentru punctajul maxim, dar facem observaţia că intersecţia a două poligoane convexe se poate face în complexitate O(N).

Aplicaţia 18: dotNet (.campion, 2004)

Se dau N puncte în planul euclidian prin coordonatele lor, numere întregi. Apoi se efectuează M operaţii asupra tuturor punctelor, într-o ordine dată (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 10 000). O operaţie poate fi de două tipuri: de translaţie sau de rotaţie. Într-o operaţie de rotaţie, punctele sunt rotite în jurul originii cu un anumit număr de grade în sens trigonometric. Într-o operaţie de translaţie, originea este mutată în alt punct relativ la originea curentă şi coordonatele celorlalte puncte sunt modificate astfel încât să reprezinte aceleaşi puncte relativ la noua origine. Scrieţi un program care calculează coordonatele tuturor punctelor după cele M operaţii.

Rezolvare:

Folosim scrierea operaţiilor de translaţie si rotaţie ca produs de matrici. Dacă vrem să rotim punctul (x, y) în jurul punctului de coordonate (0, 0) după un unghi 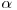atunci putem scrie:

Iar translaţia o putem scrie ca:

Astfel transformarea pentru un punct devine un produs de matrici care la sfârşit se înmulţeşte cu un vector ce reprezintă coordonatele punctului pe care vrem să îl transformăm. Pentru că transformarea compusă este aceeaşi pentru fiecare dintre cele N puncte, determinăm matricea care o reprezintă o singură dată şi apoi o putem aplica pe rând fiecărui punct. Algoritmul are complexitatea O(N + M).
Menţionăm că o problemă similară apare pe SGU sub numele de wizards, diferenţa fiind că acolo operaţiile sunt în spaţiul tridimensional, dar rezolvarea este aproape identică.

Bibliografie

1. Nicolescu, Boskoff, Probleme practice de geometrie, Ed. Tehnică, Bucureşti, 1990
2. Cut the Knot
3. Timus
4. UVa
5. TopCoder
6. SGU
7. Dijkstra’s EWDs