Revizia anterioară Revizia următoare
Solutii preONI 2008, Runda finala
Oz
Fie v vectorul de N numere care reprezinta solutia problemei. Initial consideram toate elementele vectorului v ca fiind egale cu 1. In momentul in care intalnim o pereche de forma (i j d), facem urmatoarele transformari:
- vi devine cmmmc(vi, d)
- vj devine cmmmc(vj, d),
unde prin cmmmc(a, b) se noteaza cel mai mic multiplu comun al numerelor a si b.
Acest lucru garanteaza ca atat vi cat si vj se divid prin d, si ca toate relatiile anterioare sunt respectate. In plus, deoarece alegem cel mai mic multiplu comun, stim sigur ca solutia pe care o obtinem va fi minim posibila. Este insa posibil ca cele M relatii date sa fie contradictorii. De exemplu, pentru N = 3 si relatiile (1,2,3), (2,3,6) si (1,3,1) nu vom avea solutie, deoarece din primele doua relatii stim sigur ca atat v1 cat si v3 sunt divizibile cu 3, in timp ce ultima relatie cere ca cele doua numere sa fie prime intre ele. Pentru a verifica daca intr-adevar problema are solutie este suficient, dupa ce obtinem vectorul v prin procedeul de mai sus, aplicand transformarile corespunzatoare tuturor celor M relatii, sa testam pentru fiecare triplet (i j d) daca intr-adevar cel mai mare divizor comun dintre vi si vj este d, in caz contrar neexistand solutie.
Pentru a calcula cmmmc(a, b) se foloseste relatia cmmmc(a, b) = a * b / cmmdc(a, b), iar cmmdc(a, b) se va calcula optim folosind Algoritmul lui Euclid.
Marbles
Datorita modului in care sunt mutate bilele, ordinea relativa a acestora nu se va schimba pe parcursul efectuarii operatiilor, deci ordinea culorilor va ramane neschimbata. Initial sortam bilele din fisierul de intrare dupa coordonata lor, si calculam un tablou de sume partiale S, unde Sc,i va reprezenta numarul de aparitii ale culorii c in primele i bile din lista sortata. La fiecare pas vom avea un vector de coordonate x = (x1, x2,... , xN), care, conform observatiei de mai sus, va ramane intotdeauna sortat crescator. Astfel, putem realiza operatia de mutare a unei bile in complexitatea O(log2N), cautand binar pozitia in vectorul x pe care apare bila care trebuie mutata, si modificand aceasta valoare. Daca dorim sa aflam care este numarul maxim de bile de aceeasi culoare din intervalul [i, j] este suficient sa cautam binar valorile a si b, unde a este cel mai mic numar natural astfel incat i ≤ xa, iar b este cel mai mare numar natural astfel incat xb ≤ j. Astfel, toate bilele intre pozitiile a si b inclusiv vor avea coordonata in intervalul [i, j]. Iteram fiecare culoare C de la 1 la 64 si afisam maximul valorilor de forma SC,b-SC,a-1, care reprezinta chiar numarul de aparitii ale culorii C intre pozitiile a si b.
Complexitatea algoritmului de mai sus va fi O(Nlog2N + N*C + Mlog2N + M*C). Aceasta solutie obtine punctajul maxim.
Sandokan
Observam ca elementul maxim din sir va ramane tot timpul in configuratia finala. Datorita acestul fapt, la fiecare pas putem alege elementul maxim impreuna cu alte K-1 elemente pe care le vom elimina. Deci daca configuratia finala contine P elemente, unul din cele P elemente este elementul maxim, iar restul de P-1 le putem alege in toate modurile posibile. Raspunsul la problema noastra este Combinari(N-1, P-1). Ca detaliu de implementare, puteam folosi recurenta C[n][k] = C[n-1][k-1]+C[n-1][k], obtinand complexitate O(N2) ca timp si memorie O(N) (avem nevoie doar de ultimele doua linii din matrice). O alta varianta ar fi fost sa plecam de la faptul ca 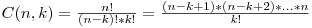 . Putem itera k de la 1 la P-1 si fiecare termen de forma n-k+i il vom imparti atat pe el cat si pe k la cmmdc(k, n-k+i). La sfarsit va trebui doar sa inmultim valorile care au ramas la numarator.
. Putem itera k de la 1 la P-1 si fiecare termen de forma n-k+i il vom imparti atat pe el cat si pe k la cmmdc(k, n-k+i). La sfarsit va trebui doar sa inmultim valorile care au ramas la numarator.
Progresii
Reformuland problema, avem de fapt N progresii aritmetice si trebuie sa gasim ratia pentru fiecare ca numarul de termeni din progresii ≤ L sa fie cel mult K. Vom construi pas cu pas solutia. La pasul i vom determina ratia progresiei i ca fiind cea mai mica posibila astfel incat daca restul progresiilor (de la i+1 la N) au ratia maxima posibila obtinem solutie. Ratia progresiei i o putem cauta binar in intervalul [1,M]. Pentru a obtine in final complexitatea O(N*logN) vom mai precalcula un vector sum[i] = numarul de termeni ≤ L daca toate ratiile de la i la N sunt egale cu M.
Peste
Sa presupunem ca la momentul x introducem in apa plasa i si vrem in viitor sa introducem si plasa j. Avem doua posibilitati: plasa j o introducem la un moment de timp mai mare decat x+T[i] sau la un moment de timp din intervalul [x,x+T[i]]. In cazul al doilea cel mai favorabil este sa introducem plasa j la momentul x. Odata ce ne hotaram ca la un moment t sa introducem in apa cateva plase este suficient sa fixam timpul maxim de asteptare (momentul la care vom scoate toate plasele introduse la momentul t) si sa consideram cel mult K plase care prind cat mai mult peste si timpul in care fac asta este mai mic sau egal decat timpul maxim fixat. Vom preprocesa un vector aux[t] = numarul maxim de pesti pe care ii putem prinde daca plasele introduse au timpul de asteptare mai mic sau egal decat t. Apoi, folosind programare dinamica vom calcula vectorul best[t] = numarul maxim de pesti pe care ii putem prinde de la momentul 0 la momentul t. Solutia se va afla in best[T]. Relatia de recurenta va fi best[t] = max(best[t-1]+aux[ 1 ], best[t-2]+aux[ 2 ]...best[t-TMAX]+aux[TMAX]). Complexitatea solutiei va fi O(N*logK+T*TMAX), unde TMAX este timpul maxim de asteptare a unei plase (in cazul nostru 1000). Pentru a preprocesa vectorul aux[] putem folosi un heap sa obtinem complexitatea acestui pas O(N*logK).
Wanted
Problema se va rezolva folosind programare dinamica. Vom considera satele sortate dupa ordonata X. Vom construi matricile
- Ai,j - distanta minima parcursa pentru a rezolva intervalul i...j si daca ne-am afla initial in satul i-1
- Bi,j - distanta minima parcursa pentru a rezolva intervalul i...j si daca ne-am afla initial in satul j+1
Relatia de recurenta se poate observa usor. Fixam pe rand fiecare sat k pe care il vom vizita prima oara si ne uitam la Ak+1,j si Bi,k-1, alegand maximul dintre cele doua (luam in coniderare doar cazul cel mai defavorabil). Dintre toate posibilitatile de a alege k o vom retine pe cea care da rezultatul minim.
Pentru a stabili rezultatul fixam din nou k, primul sat vizitat si alegem minimul dintre toate posibilitatile.
Complexitatea algoritmului va fi O(n3).
Sortare
Presupunem ca avem o permutare de lungime n si pozitiile An, Bn si Cn. Vom considera doua cazuri:
- An ≠ Bn ≠ Cn
In cazul in care cei trei indici sunt diferiti este evident ca nu poate aparea ca pivot numarele 1 sau n, deoarece nu exista numere mai mici, respectiv mai mari decat ele. In schimb, putem construi sirul astfel sa apara ca pivot orice numar de la 2 la n-1. Deoarece vrem ca adancimea sa fie maxima, trebuie ca una din cele doua bucati care se obtin dupa partititonare sa fie cat mai mare. Asadar, are rost sa punem ca pivot doar 2 sau n-1, reducand rezolvarea pentru lungimea n la rezolvarea lungimii 1 si lungimii n-2. - An = Bn sau An ≠ Cn sau An ≠ Bn
In cazul in care cel putin doi din indici sunt egali putem aplica un rationament ca cel de mai sus, doar ca de data asta putem pune ca pivot si numerele 1 si n. Astfel, rezolvarea pentru lungime n se reduce la rezolvarea lungimii n-1.
Pe baza acestor doua observatii putem face o rezolvare recursiva care alege pivotul in mod greedy in functie de cele doua cazuri. Complexitatea rezolvarii este O(N2).
Vanatoare
Problema se rezolva cu ajutorul programarii dinamice. Sa notam cu Mi multimea {j | al j-lea bit din reprezentarea lui i in baza 2 este 1}. Fie Di numarul minim de vanatori necesari pentru a omori toti mistretii cu numere de ordine din multimea Mi. Relatia de recurenta va fi Di = 1 + minim(DMi-Mj), dupa toate numerele j cu proprietatea ca multimea Mj este inclusa in multimea Mi si toti mistretii din Mj pot fi omorati de acelasi vanator, situat la o coordonata intre 0 si T. Pentru a stabili daca toti mistretii din Mj pot fi omorati de acelasi vanator, vom realiza o preprocesare. Astfel, Ai va fi true daca si numai daca putem plasa un vanator intre 0 si T care sa omoare toti mistretii din Mi. O optimizare evidenta care imbunatateste cu mult timpul de executie este ca pentru o stare i sa eliminam acele j despre care stim sigur ca Aj va fi false. Astfel, daca la un moment dat alegem un numar j pentru care Aj va fi false nu are rost sa consideram nici un numar k, pentru care Mj inclus in Mk, pentru ca Ak va fi sigur false.
Pentru a calcula valoarea lui Ai trebuie sa determinam cel mai mic numar natural P (daca exista) astfel incat vanatorul plasat in P sa poata omori toti mistretii din Mi. Aceasta relatie este echivalenta cu P % vj = cj, pentru orice j inclus in Mi. Pentru a afla numarul P pentru o stare i putem folosi teorema chineza a resturilor. Nu este necesar insa sa aplicam aceasta teorema de la inceput pentru fiecare stare, ci este suficient sa vedem care este ultimul bit j de 1 din i, si sa combinam solutia pentru Mi-{j} si {j}. Ai va fi true daca si numai daca 0 ≤ P ≤ T.
Complexitatea finala va fi O(2N * N) + O(3N) = O(3N).
Talharie
Vom numerota caracterele din sir de la 0 la N-1. Vom identifica o rotatie a sirului prin indecele asociat caracterului cu care respectiva rotatie incepe. Notand cu D cel mai mare divizor comun al numerelor N si K, putem demonstra folosind notiuni elementare de teoria numerelor ca toate rotatiile pe care le putem obtine efectuand operatia descrisa in enunt sunt multiplii ai lui D. Folosindu-ne de faptul ca diferenta intre oricare doua rotatii consecutive care ne intereseaza este constanta, putem foarte usor sa modificam cei doi algorimti prezentati in articolul scris de Mircea Pasoi. Pentru a obtine 100 de puncte, era suficienta implementarea algoritmului de complexitate O(N * log N).


