Soluţii ONIS 2016, Runda 1

• Lista de probleme
• A. MaxSubSum
• B. Avioane2
• C. Minlcm
• D. Unlock
• E. Min Max Store
• F. Pokemon3
• G. Puzzle2
• H. Subpermutari
• I. Nucleul Valoros Season 2

Cine a rezolvat o problema a carei solutie nu este inca adaugata, este rugat sa o scrie in sectiuniile de mai jos :)

A. MaxSubSum

Datorita limitei lui N (N <= 2.000), solutia triviala in care matricea este calculata iar apoi este aplicat algoritmul pentru submatrice de suma maxima O(N³) nu va intra in timp.
Se observa ca orice submatrice este de fapt data de o subsecventa din primul sir S1 si o subsecventa din al doilea S2. Suma elementelor a submatricei este de fapt len(S1) * sum(S2) + len(S2) * sum(S1).
Se va calcula pentru fiecare sir max[i] = suma maxima a unei subsecvente de lungime i in O(N²).
Avand max1 si max2 (pentru cele doua siruri), in O(N x M) putem incerca toate lungimile L1, L2 (1 <= L1 <= N, 1 <= L2 <= M) de secvente posibile pentru cele doua siruri iar cu formula de mai sus putem calcula suma maxima ce se poate obtine pentru lungimile respective. Vom salva si afisa valoarea maxima. Complexitatea finala este O(N² + M² + N x M)

B. Avioane2

Din zborurile care sunt date, se construieste un graf in care nodurile sunt perechi de forma 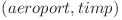. Sunt suficiente numai perechile din zborurile initiale (cel mult 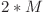perechi, deci tot atatea noduri), plus inca o pereche 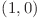(aeroportul 1, timpul 0) de la care se porneste.

Muchiile se leaga in felul urmator:
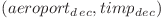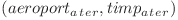1. intre nodurile de forma si (intre care exista zbor) se leaga o muchie avand costul 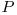corespunzator zborului. Se obtin 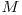muchii de zbor;
2. intre nodurile corespunzatoare aceluiasi aeroport se leaga muchii cu cost (costul de asteptare) de la nodul cu timp mai mic la nodul imediat urmator ca timp. De exemplu, daca pentru aeroportul 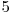am zboruri (care ajung sau pleaca) la timpii , , 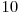, , 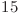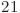se vor pune muchii intre perechile: 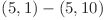, , 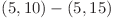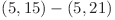. Daca cei doi ajung in aeroportul 5 la timpul 10 si vor sa plece la timpul 21, drumul 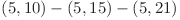va corespunde asteptarii si va avea cost 0. Se obtin cel mult 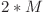muchii de asteptare.

In continuare, se utilizeaza un algoritm de drum de cost minim (Dijkstra sau Bellman-Ford) de la nodul de plecare 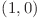la toate celelalte noduri pentru a putea afla costul minim de a ajunge la un anumit aeroport la un anumit moment de timp.

Acum pentru fiecare query de forma 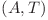(aeroport, timp) se afiseaza minimul dintre distantele pana la toate nodurile 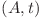, unde 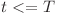sau 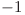daca nu exista astfel de noduri sau nu pot fi atinse. Pentru asta exista mai multe variante, de exemplu cu sortarea query-urilor si rezolvarea lor offline sau aplicand cautare binara.

C. Minlcm

Observam ca cmmmc(a, b) = a * b / cmmdc(a, b). Astfel, daca fixam cmmdc(a, b), perechea de multiplu comun minim are produsul minim.
Pentru a afla perechea aceasta, vom utiliza un algoritm asemanator cu ciurul lui Eratostene, fixand cel mai mic multiplu comun al perechii alese, si alegand cei mai mici doi multiplii ai acestui numar.

D. Unlock

Pentru rezolarea acestei probleme, vom folosi o structura de date speciala: o padure de multimi disjuncte care ne permite sa anulam ultimele operatii. Pentru realizarea acesteia, se retine o stiva cu operatiile facute.
Vom verifica pentru fiecare culoare daca este un unlocker. Vom creea o padure de multimi disjuncte cu anulari in care elementele nodurilor reprezinta spatiile matricii. Initial, toate spatiile libere vecine vor fi legate. Sa zicem ca culoarea pentru care verificam este c. Vom adauga toate spatiile de culoare c, legandu-le de vecinii de culoare c sau liberi. Verificam, apoi, daca o componenta care contine un spatiu liber le contine pe toate (pentru aceasta poate fi utilizata o stare suplimentara care contine numarul de spatii libere din multime). Daca da, atunci culoarea c este un unlocker, altfel nu. Observam ca adaugam si scoatem (prin anulare) fiecare element al matricii o data. Astfel, algoritmul are complexitatea O(n^2 * (comlexitate_uneste + complexitate_anuleaza)). Era suficienta pentru 100 de puncte o implementare cu complexitate_uneste = O(logn), complexitate_anuleaza = O(1).

E. MinMaxStore

Vom explica doar modul in care determinam daca pozitia de minim este corecta (pentru maxim modul de gandire este acelasi).

Parcurgem operatiile de la sfarsit spre inceput si mentinem un set S care la fiecare moment va contine pozitiile pe care minimul din permutare ar trebui sa se afle pentru ca la final acesta sa fie pe pozitia PMIN.
Mai formal, daca dupa operatia i (cu i de la M la 0), minimul se afla pe pozitia pos si pos ∈ S, atunci la final minimul se va afla pe pozitia PMIN.
Daca minimul se afla pe pozitia pos si pos ∉ S, atunci la final minimul nu se va afla pe pozitia PMIN.

Dupa operatia M, singura pozitie valida pentru minim este PMIN. Astfel S = {PMIN} initial.

Presupunem ca la acest moment stim cum arata S dupa operatia i si vrem sa aflam cum arata S dupa operatia i - 1. Fie (Ai, Bi) operatia STORE cu numarul i. Se disting 3 cazuri:

  a)  Ai ∈ S => S = S ∪ {Bi}  (daca minimul se afla in Bi, acesta va trece in Ai si cum Ai este in S, va ajunge la final pe PMIN).

  b)  Ai ∉ S, Bi ∈ S => S = S \ {Bi}  (daca minimul se afla in Bi, acesta va trece in Ai si cum Ai nu este in S, acesta nu va mai ajunge la final pe PMIN)

  c)  Ai ∉ S, Bi ∉ S => S nu se modifica

La final (dupa operatia 0, adica inainte de orice operatie), daca S contine toate pozitiile din vector (de la 1 la N), atunci pozitia de minim e corecta. Altfel, nu.

Complexitatea per test va fi O(M * log(N)) daca se foloseste set, respectiv O(M) pentru unordered_set.

F. Pokemon3

O observatie importanta este ca pentru a castiga "din prima" Ash va alege (din lista sa de pokemoni) la fiecare lupta un pokemon care este super eficient fata de cel al adversarului. Asta inseamna ca nu conteaza ordinea bataliilor ci doar tipurile de pokemoni adversi ce trebuie infranti. Datorita limitei mici a lui N (N <= 20) se pot incerca toate posbilitatile de a alege pokemonii (backtracking). O configuratie (un anume grup de pokemoni alesi) se considera valida daca nu exista niciun pokemon advers ce nu poate fi infrant folosindu-ne de pokemonii din configuratia curenta. Se va retine numarul cel mai mic de pokemoni din configuratiile valide. Complexitatea solutiei, data de backtracking, este de O(2^N).

G. Puzzle2

O solutie simpla se bazeaza pe urmatoarea observatie: sa zicem ca am gasit pozitiile tuturor pieselor pana la un rand r0 dat, r0 < R. Este usor sa generam randul r0+1, caci fiecare element de pe randul r0 are exact un vecin care nu este deja utilizat. Astfel, primul element de pe r0+1 va fi vecinul neutilizat al primului element de pe r0, s.a.m.d.
Primul rand se genereaza plecand de la un colt, care poate fi gasit pe baza numarului de vecini. Trebuie tratate cazurile speciale in care C = 1 si C = 2.

H. Subpermutari

Consideram toate cele N² subsecventele are permutarii noastre. Observam faptul ca daca pentru o secventa [a,b] determinam cea mai lunga subpermutare care este atat prefix, cat si sufix a secventei noastre, putem foarte usor marca sufixul ca fiind o secventa care a mai aparut deja si crestem frecventa prefixului.
Pentru a determina cea mai lunga subpermutare care este atat prefix, cat si sufix, vom aplica un algoritm foarte asemanator KMP-ului:
Fixam pozitia de start a subsecventei noastre si pornim algoritmul de KMP de acolo.
Presupunem ca avem calculat pentru o subsecventa [a,b] acest cel mai bun prefix-sufix (il notam identic ca la KMP cu pi[b]). Cand vrem sa trecem la urmatorul element, b + 1, avem aceleasi 2 cazuri de luat in considerare ca si la KMP:

Cazul in care elementul inserat b + 1 are aceelasi indice in subpermutarea sufixului ca si urmatorul element in subpermutarea prefixul: pur si simplu pi-ul creste cu 1
Daca indicele difera, micsoram pi-ul (mergem in pi[pi[b]]) si repetam procedeul pana avem o potrivire

Pentru a determina al catelea element se afla o valoare intr-o secventa putem usor precalcula cu un simplu aib.
Complexitate: O(N² log N)

I. NucleulValoros2

Se consideră:



Această recurenţă se poate calcula în 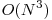, dar nu este de ajuns pentru această problemă. Se observă că are următoarele proprietăţi:




Aceste proprietăţi sunt necesare, dar şi suficiente pentru a aplica optimizarea Knuth-Yao, care reduce complexitatea la