Training Dummy

Avand o secure cu puterea 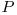P si o papusa cu 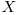X puncte de viata, avem nevoie de 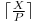\lceil\frac{X}{P}\rceil lovituri pentru a distruge papusa. Deci, numarul mediu de secunde este egal cu \sum\limits_{i=A}^{B}P(\text{securea echipata are puterea i})\cdot\lceil\frac{X}{i}\rceil = \sum\limits_{i=A}^{B}\frac{1}{B-A+1}\cdot\lceil\frac{X}{i}\rceil = \frac{1}{B-A+1} \sum\limits_{i=A}^{B}\lceil\frac{X}{i}\rceil.
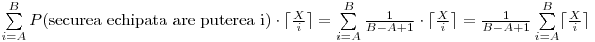Solutia are complexitatea 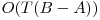O(T(B-A)).

Super Mario

Solutia 1

Definim o functie 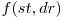f(st, dr) care returneaza numarul minim de mutari necesare pentru a distruge toate testoasele din intervalul [st, dr], folosind numai testoase din acest interval. Raspunsul va fi dat de f(1, N).
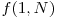In continuare, incercam sa gasim raspunsul pentru intervalul [st, dr]. Pe care testoasa o distrugem prima si in ce directie o impingem?
Fie 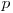p pozitia testoasei din acest interval cu puterea maxima. Observam ca la prima mutare o vom alege tot timpul pe aceasta. Nu are rost sa incepem cu alta testoasa, deoarece avem sansa sa ne lovim de tesoasa 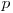p si in acest caz era mai bine sa inversam ordinea mutarilor.
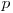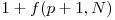Deci, distrugem testoasa p si incercam sa o impingem in ambele directii. Daca o impingem spre stanga, distrugem toate testoasele din intervalul [st, p-1]. In acest caz avem nevoie de 1 + f(p+1, N) mutari. Similar, daca o impingem spre dreapta, avem nevoie de 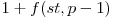1 + f(st, p-1) mutari. Deci, 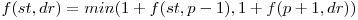f(st, dr) = min(1 + f(st, p-1), 1 + f(p+1, dr)). Cazul de baza este st > dr.
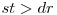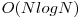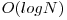Aceasta solutie are complexitatea O(NlogN), deoarece in cel mai rau caz vizitam N intervale si pentru fiecare aflam maximul in O(logN). Maximul se poate afla cu arbori de intervale sau cu range minimum query.

Solutia 2

Aceasta solutie se bazeaza pe programare dinamica. Precalculam doi vectori left si right cu semnificatia left[i] = testoasa cea mai din dreapta care se afla in stanga testoasei i si are puterea mai mare ca aceasta. Formal, left[i] = max(j | j < i si P[j] > P[i]). Similar, right[i] = min(j | j > i si P[j] > P[i]).
Definim starea ca si dp[i] = numarul minim de mutari necesare pentru a distruge primele i testoase. Pentru fiecare testoasa i pe care o distrugem avem doua variante:

  • O impingem spre stanga. Distrugem toate testoasele din intervalul [left[i]+1, i], deci dp[i+1] = min(dp[i+1], 1 + dp[ left[i]+1 ]).
  • O impingem spre dreapta. Distrugem toate testoasele din intervalul [i, right[i]-1], deci dp[ right[i] ] = min(dp[ right[i] ], 1 + dp[i]).

Raspunsul se afla in dp[N].
Vectorii left si right se pot precalcula cu ajutorul unei stive in O(N). Complexitatea finala a acestei solutii este O(N).

Hero's Call: Northrend!

In continuare, vom considera fiecare oras din cele N ca fiind un nod, iar fiecare portal ca fiind o muchie care conecteaza doua noduri, in schimbul unui cost. Asadar, este destul de evident ca structura noastra este un arbore cu N noduri.

Vom construi toate drumurile posibile "invers", folosind o parcurgere in adancime din nodul X. Vom parcurge toate nodurile vecine cu nodul X. Avem doua cazuri:

  • Muchia (Y, X) are cel mai mic cost dintre muchiile conectate de nodul Y. Deci, in nodul Y am fi putut ajunge prin oricare alt nod conectat de el, in afara de X.
  • Muchia (Y, X) este a doua in sirul muchiilor sortate crescator dupa cost, conectate de nodul Y. Deci, este evident ca in nodul Y am ajuns prin muchia minima din acest nod.
  • Altfel, 

Temple

Construim un arbore in care tatal nodului x este Next[x]. Astfel, observam ca S[x] este, de fapt, maximul din valorile primilor K stramosi ai lui x. Pentru a calcula aceste valori, putem face o parcurgere DFS, sa retinem nodurile de pe lantul curent intr-o stiva si sa mentinem o structura de date (multiset, arbore de intervale etc.) cu valorile ultimelor K noduri de pe lant.

Complexitatea de timp este O(N * logN), iar memoria folosita este O(N).