LCA: Lowest common ancestor
(Categoria Algoritmi, Autor Emilian Miron)
Problema luata in discutie este ca, avand un arbore dat, sa putem raspunde rapid la multe intrebari de genul: "Care este stramosul comun cel mai apropiat dintre doua noduri din arbore?".
- Continut
- Exemplu
- Aplicabilitate
- Mod de calcul
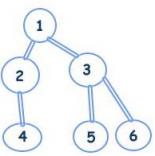
Exemplu
Pentru arborele din imagine, avem ca exemplu urmatoarele query-uri:
- lca(2,3) = 1
- lca(4,5) = 1
- lca(5,6) = 3
- lca(1,5) = 1
- lca(5,3) = 3
Aplicabilitate
Dandu-se un arbore cu costuri sa se raspunda rapid la intrebari de genul: "care este distanta minima intre doua noduri date?". O solutie pentru problema de fata ar fi:
- agatam arborele intr-un nod oarecare si obtinem un arbore cu radacina
- pentru fiecare nod i precalculam disti, reprezentand distanta sa pana la radacina
- precalculam cele necesare pentru algoritmul de Lowest Common Ancestor
- distanta dintre doua noduri oarecare i si j va fi egala cu disti + distj - 2*distlca(i,j)
Mod de calcul
In prima etapa a algoritmului facem o parcurgere euleriana a arborelui dat. O parcurgere euleriana este o parcurgere a arborelui in ordinea din figura: se parcurg fiii si se intercaleaza intre ei tatal, obtinand o parcurgere continua.
Mai exact pentru fiecare nod procedam astfel, incepand cu radacina:
- daca nodul curent este frunza il adaugam la parcurgere
- daca are fii atunci il punem la inceput, la sfarsit si intre parcurgerile euler ale fiilor
Cand facem aceasta parcurgere retinem de asemenea si urmatoarele informatii suplimentare:
- adancimea fiecarui nod din parcurgere, obtinand un sir de adancimi
- una din pozitiile pe care fiecare nod apare in parcurgere
Ideea este ca lca(i, j) este chiar nodul cu cea mai mica adancime intre pozitiile lui i si a lui j in parcurgere. Pentru graful din figura de mai sus avem:
| Euler | Adancimi |
|---|---|
| 12421353631 | 12321232321 |
Pentru perechea de noduri (4, 3), avem lca(4, 3) egal cu nodul care se gaseste intre poz4 si poz3 in parcurgerea euler si are adancimea minima. Acest nod este 1, deci lca(4, 3) = 1.
Am redus problema la aflarea minimului intre doua pozitii ale unui sir (Range Minimum Query). Aceasta subproblema o putem rezolva optim folosind arbori de intervale, sau o metoda folosind spatiu supraliniar (Nlog2N) a minimelor pe intervale de puteri ale lui 2, incepand de la pozitia i. Timpul de preprocesare este O(N) pentru arbori de intervale si O(Nlog2N) pentru a doua metoda. In ambele variante timpul de interogare este O(log2N).
Vom prezenta in continuare metoda cu spatiu supraliniar. Calculam minimele inductiv, pastrand:
- mini,k = minimul pe intervalul [i...i+2k-1] (de lungime 2k), si
- minposi,k = pozitia minimului de pe intervalul [i...i+2k-1].
Acest tablou va fi construit recursiv astfel: pentru k = 0 avem mini,0 = ai si minposi,0 = i, iar pentru k > 0 avem:
- mini,k = minim(mini,k-1, mini+2k-1,k-1)
- minposi,k = pozitia minimului (minposi,k-1 sau minposi+2{k-1},k-1)
Pentru query intre pozitiile l si r procedam astfel: fie k cel mai mare numar astfel incat 2k ≤ lungimea intervalului (l, r).
min(l, r) = minim( minl,k, minimul pe intervalul (l+2k, r))
pozmin(l, r) = pozitia minimului intre l si r
Daca l = posi si r = posj (posi < posj) la sfarsitul query-ului eulerpozmin este chiar lca(i, j).
