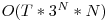Soluţii Grigore Moisil 2011
Inel
Problema se reduce la a determina numărul permutărilor de lungime N, astfel încât pe prima poziţie să avem valoarea 1, iar suma a oricare două numere consecutive din şir să fie un număr prim. Şi pentru că în inel primul număr cu ultimul sunt vecini, va trebui să mai testăm dacă ultimul număr din şir adunat cu primul au ca rezultat un număr prim.
Permutările unui şir se generează cu metoda backtracking. Pentru a obţine punctajul maxim vor trebui testate condiţiile pe parcursul construirii şirului.
Complexitate: 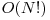
Inundaţie
Solutia 1
Problema se poate rezolva cu ajutorul unui arbore binar de cautare. In fiecare nod al arborelui se va pastra:
- Valoarea nodului ( val )
- Numarul de aparitii a valorii in matrice ( nr )
- Numarul de numere mai mari strict decat valoarea de pe nodul respectiv ( nrhigh )
- Suma tuturor numerelor strict mai mici decat valoarea de pe nod ( sumlower )
Adaugarea se face in O(N*logN).
De fiecare data se cauta valoarea etajului pana la care se va adauga minus o unitate ( V etaj - 1 ) in arborele de cautare. De fiecare data se adauga intr-o variabila contor - ( nrhigh + nr )*( V etaj - 1 ) daca valoarea cautata este mai mica decat valoarea nodului pe care ne aflam, sau sumlower + ( nr * val ) , daca valoarea pe care o cautam este mai mare decat valoarea nodului. Sunt doua situatii in care se poate opri cautarea:
- S-a ajuns la valoarea cautata si in cazul acesta se contorizeaza nrhigh * ( V etaj - 1 ) + sumlower + nr * val
- Nu s-a gasit valoarea cautata si s-a ajuns la un NULL, in cazul acesta se opreste cautarea pur si simplu
Valoarea contorului va fi numarul de locuinte inundate la final.
Deoarece adaugarea se face in O(N*logN) si cautarea in O(logN), complexitatea finala este O(N*logN + Q*lonN).
SumDiv2
Soluţie de 20 pct
Pentru început, prezentăm o soluţie trivială care rezolvă problema pentru fiecare interval parcurgând toate elementele intervalului. Pentru fiecare număr din interval, calculăm suma divizorilor numărului. Pentru a afla suma divizorilor unui număr X, prelucrăm toate numerele Y din intervalul [1..[sqrt(X)]] şi calculăm restul împărţirii lui X la Y. Dacă restul este 0, avem doi divizori: Y şi [X/Y]. Desigur, trebuie avut grijă ca în cazul în care X este pătrat perfect să nu se contorizeze [sqrt(X)] de două ori. ( [X] reprezintă parte întreagă din X )
Complexitate: 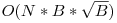
Soluţie de 50 pct
Citim iniţial toate intervalele şi le salvăm în memorie. În timp ce le citim, determinăm în maxB valoarea maximă a capetelor B ale tuturor intervalelor. Vom crea un vector P, unde în P[i] vom păstra suma divizorilor numărului i, sumă determinată cu metoda explicată la soluţia anterioară. Vom crea un nou vector Q[i] = P[1] + P[2] + … + P[i]. Recurenţa este următoarea: Q[i] = Q[i-1] + P[i].
Astfel, răspunsul corespunzător unui interval se află în timp constant. Mai exact, suma divizorilor tuturor numerelor din intervalul [st, dr] este Q[dr] – Q[st] – 1.
Complexitate: 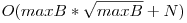
Soluţie de 100 pct
Determinăm valoarea lui maxB ca la soluţia anterioară. Construim vectorul P, unde P[i] = suma divizorilor numărului i prin metoda ciurului lui Eratostene. Mai exact, ştim că fiecare număr i din intervalul [1, maxB] este divizor al său şi al tuturor multiplilor săi. Astfel, vom incrementa cu i elementele P[i], P[2*i], P[3*i], … Utilizând vectorul P ca în soluţia anterioară, vom crea vectorul Q şi vom răspunde în timp constant.
Complexitate: 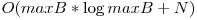
Dreptunghiuri3
Soluţie de 20 pct
Se parcurge fiecare poziţie din matrice, şi se verifică cu ce dreptunghiuri se intersectează.
Complexitate: 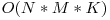
Soluţie de 50 pct
Vom folosi o matrice DP de dimensiune N * M, cu valoarea 0 în toate poziţiile. Pentru fiecare dreptunghi citit, se fac următoarele modificări asupra matricei:
DP[i1][j1] += v, DP[i2+1][j2+1] += v;
DP[i2+1][j1] -= v, DP[i1][j2+1] -= v;
Acum, valoarea fiecărei căsuţe (i, j), este suma tuturor valorilor din DP[x][y], cu x ≤ i şi y ≤ j.
Complexitate: 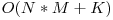
Soluţie de 100 pct
Ne vom folosi de ideea de la soluţia anterioară, doar că vom normaliza datele de intrare. Se observă că pentru fiecare dreptunghi, ne interesează doar liniile i1, i2, i2+1, şi doar coloanele j1, j2, j2+1. Deci vom forma doi vectori:
Lin = {i1, i2, i2+1}, pentru toate dreptunghiurile
Col = {j1, j2, j2+1}, pentru toate dreptunghiurile
Ordonăm crescător cei doi vectori şi eliminăm valorile duplicate.
Acum, la construcţia matricii DP, linia i1 va deveni posLin(i1), linia i2 va deveni posLin(i2) iar linia i2+1 va deveni posLin(i2+1). Prin posLin(x) am notat poziţia valorii x în vectorul sortat Lin. Desigur, acelaşi lucru se va face pentru coloane, şi deci vom avea o matrice DP cu cel mult 3*K linii şi cel mult 3*K coloane. Trebuie acordată mare atenţie la calcularea numărului de câsuţe, deoarece acum o căsuţă din DP poate reprezenta mai multe căsuţe din matricea noastră.
Complexitate: 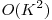
Stup
Fiecărei albine îi găsim vecinii pentru a forma un graf pe care îl folosim mai târziu. Acest lucru se poate face simplu în 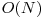 timp şi memorie. Ştim că fiecare albină are 6 vecini, excepţie făcând albinele aflate pe conturul stupului. Când vrem să aflăm vecinii unei albine, ne putem uita doar la albinele cu număr de ordine mai mare, deoarece ceilalţi sunt deja adăugaţi. Să considerăm albina X. Ştim cu siguranţă că X+1 îi va fi vecin. Restul vecinilor pot fi determinaţi cu ajutorul vecinilor lui X-1. Ultimul său vecin adăugat va fi şi el vecin pentru X. Să îl numim V. Cât timp X nu are 6 vecini continuăm să îi inserăm în lista de adiacenţă pe V+1, V+2, ...
timp şi memorie. Ştim că fiecare albină are 6 vecini, excepţie făcând albinele aflate pe conturul stupului. Când vrem să aflăm vecinii unei albine, ne putem uita doar la albinele cu număr de ordine mai mare, deoarece ceilalţi sunt deja adăugaţi. Să considerăm albina X. Ştim cu siguranţă că X+1 îi va fi vecin. Restul vecinilor pot fi determinaţi cu ajutorul vecinilor lui X-1. Ultimul său vecin adăugat va fi şi el vecin pentru X. Să îl numim V. Cât timp X nu are 6 vecini continuăm să îi inserăm în lista de adiacenţă pe V+1, V+2, ...
Mai departe, vom forma un nou graf cu ajutorul celui descris anterior. Fiecare nod din graful nou reprezintă un trib, iar muchiile sale duc în triburile vecine. Acest lucru se poate face în 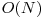 . Pentru a afla numărul minim de triburi facem o parcurgere în lăţime pe acest graf.
. Pentru a afla numărul minim de triburi facem o parcurgere în lăţime pe acest graf.
Poligon5
În primul rând vom încerca să aflăm punctele de coordonate întregi de pe fiecare latură în parte. Să luăm cele două puncte care delimitează segmentul, le putem nota cu P1(X1,Y1) şi P2(X2,Y2). Fie dx = |X1-X2| şi dy = |Y1-Y2|, dx este diferenţa dintre puncte pe axa Ox, iar dy pe axa Oy. Este cunoscut faptul că numărul de puncte laticeale de pe segment este cmmdc(dx,dy) – 1 (fără să luăm în calcul extremităţile), iar fiindcă acestea sunt distribuite pe orice latură la intervale egale, aflarea lor este facilă odată aflat cmmdc(dx,dy).
În continuare fixăm un vârf de start al noului poligon (facem asta luând pe rând toate punctele de pe o latură) şi calculăm perimetrul minim folosind programare dinamică. Semnificaţia stării este perimetrul minim al poligonului „parţial” cu vârfurile de start şi de sfârşit fixate.
Ignorând vârful de start, dinamica arată în felul următor:
PMIN[p] = PMIN[p'] + Dist(p, p')| p' aparţine laturii care precede latura pe care se află p.
unde p, p' sunt puncte de coordonate întregi.
Analiza complexităţii:
Fie N numărul de puncte laticeale şi nrlat numărul de laturi ale poligonului iniţial.
Fixarea primului vârf al poligonului: este optim să alegem primul vârf al poligonului dintre punctele laticeale de pe latura cu cele mai puţine puncte. Observăm că în cel mai rău caz acest număr nu depăşeşte N/nrlat.
Rezolvarea recurenţei: În recurenţă vom găsi drumul minim până la un punct laticeal pe care îl fixăm ca vârf al poligonului. Pentru aflarea drumului minim trebuie să găsim amplasarea optimă a vârfului care precede vârful curent. Vom analiza toate variantele, deci trebuie să ne uităm la toate punctele de pe latura care precede latura pe care se află vârful curent. Amortizat, acest calcul are complexitatea 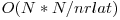 .
.
În cea mai nefavorabilă distribuţie a punctelor laticeale pe laturile poligonului iniţial, avem în jur de N3/9 operaţii (cazul în care nrlat = 3), deci complexitatea finală este 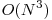 .
.
Cărţi2
Putem rezolva problema folosind programare dinamică. O stare a dinamicii va fi înălţimea minimă necesară unei biblioteci de lăţime L care să cuprindă o parte din cărţile date, adică o submulţime a lor. Răspunsul la problemă va fi submulţimea de cărţi de cardinal maxim şi minim lexicografică care încape într-o bibleotecă mai mică sau egală ca înălţime decât cea dată. Pentru o submulţime oarecare de cărţi pe care le alegem să le plasăm în bibliotecă, determinăm înălţimea minimă necesară bibliotecii ca să le cuprindă. Din această submulţime alegem încă o submulţime inclusă în ea şi care încape pe un raft. Pentru cărţile pe care nu le luăm în submulţimea nouă ştim deja înălţimea minimă şi astfel am găsit recurenţa:
![Hmin[C] = (max(A_i), i \in C') + G + Hmin[C - C'], \displaystyle\sum_{i \in C'}\ B_i \le L Hmin[C] = (max(A_i), i \in C') + G + Hmin[C - C'], \displaystyle\sum_{i \in C'}\ B_i \le L](https://www.infoarena.ro/static/images/latex/0bd890e053d3f6b6d10f1a660f943a5b_14.47978pt.gif)
C : submulţime de cărţi
C' : submulţime a mulţimii C
Restul notaţiilor sunt preluate din enunţ.
Complexitate finală: