Revizia anterioară Revizia următoare
Eliminare Gaussiană
(Categoria Algoritmi, Autor Petru Trîmbiţaş)
- Conţinut:
- Descriere
- Aplicaţii
- Bibliografie
Descriere
Eliminarea Gaussiană este o metodă de rezolvare a ecuaţiilor matriciale de forma 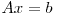 .
.
Să presupunem că avem următorul sistem:
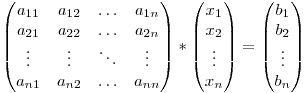
Pentru a rezolva sistemul vom transforma toate elementele de sub diagonala principală a matricei extinse în 0.
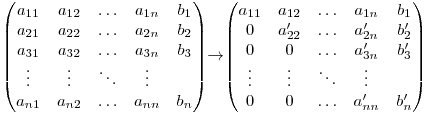
Având matricea sub această formă putem să aflăm uşor necunoscutele:
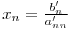
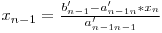
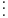
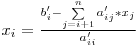
Aplicaţii
The magic matrix
https://apps.topcoder.com/wiki/display/tc/TCO+2013+Round+2A#TheMagicMatrix
Go2
Gxor
Bibliografie
- http://en.wikipedia.org/wiki/Gaussian_elimination
- http://mathworld.wolfram.com/GaussianElimination.html
