Revizia anterioară Revizia următoare
Deque şi aplicaţii
(Categoria Structuri de date, Autor Xulescu)
În acest articol voi prezenta o structură de date de tip listă numită deque. Simplitatea acestei structuri poate nu are multe de spus şi din acest motiv am prezentat şi o serie de aplicaţii care vor arăta neaşteptata sa utilitate şi apariţie în locurile unde am fi crezut că nu se mai poate face nimic pentru a reduce complexitatea.
Introducere
Dequeul (pronunţat de obicei deck) poate fi privit ca o colecţie de tip listă ce are două capete prin care se şterg sau inserează noi elemente. În literatura de specialitate, aceste capete se numesc head şi tail, iar dequeul mai este recunoscut şi ca fiind o coadă cu două capete (double ended queue).
Un deque poate fi implementat folosind liste dublu înlănţuite, sau cu un vector static când se cunoaşte numărul elementelor din colecţie. Ce trebuie reţinut este că limbajul C++ pune la dispoziţia utilizatorilor prin intermediul headerului #include <deque> clasa std::deque.
Operaţii
Mai jos sunt enumerate operaţiile care pot fi efectuate asupra unui deque împreună cu corespondentul lor în limbajul C++:
- front(): întoarce primul element;
- back(): întoarce ultimul element;
- push_front(): inserează un element în faţă;
- push_back(): inserează un element în spate;
- pop_front(): scoate primul element;
- pop_back(): scoate ultimul element;
- empty(): întoarce true dacă dequel este gol.

Toate aceste operaţii se execută în timp O(1) amortizat. Pentru un plus de viteză va trebui să folosim un vector static cu dimensiunea egală cu numărul maxim de elemente ce pot trece prin deque, iar operaţiile implementate „de mână”, cu doi indecşi ce indică către head şi tail. Însă, în majoritatea aplicaţiilor limita de timp permite folosirea lejerităţii şi siguranţei clasei std::deque.
Aplicaţii
În multe aplicaţii unde soluţiile parţiale se reprezintă sub forma unui şir continuu de valori care permite inserarea şi ştergerea doar pe la capete (în general inserări pe la un capăt şi ştergeri pe la celălalt) se poate folosi un deque. Să urmărim în continuare cazuri concrete în care simplitatea unui deque duce la soluţii de multe ori optime şi implementări foarte scurte şi clare.
Problema 1: Book Pile (SGU)
Se dau N cărţi aşezate una deasupra celeilalte asupra cărora se vor efecta M operaţii de două tipuri: 1. ADD(nume) : se adaugă cartea nume deasupra celorlalte; 2. ROTATE : primele K cărţi de deasupra se rotesc (dacă sunt mai puţin de K cărţi atunci se vor roti toate). Se cere să se afişeze cărţile în ordine, prima fiind cea de deasupra, după efectuarea celor M operaţii.
Restricţii: 0 ≤ N, K ≤ 40 000, 0 ≤ M ≤ 100 000.
Soluţie:
Soluţia problemei se poate deduce urmând paşii următori. Să presupunem că avem cărţile A B C iniţial şi K = 3. Dacă îl vom adăuga pe D, atunci nu vor rămâne importante decât cărţile D A B, deoarece, dacă vom roti ulterior ultimele K cărţi, C nu va mai fi niciodată considerat, cărţile fiind doar adăugate, iar o dată ce o carte iese din „top K” cărţi nu va mai fi posibil să i se schimbe poziţia pe raft. Să rotim acum „top K” cărţi. Noua ordine va fi B A D şi C pe raft la loc sigur. Dacă îl vom adăuga pe E, topul se va schimba în E B A iar pe raft, în mod sigur vor fi, în această ordine, D C. Proprietatea celor K cărţi din vârf este: o secvenţă continuă de elemente, la care se adaugă noi elemente sau se elimină dintre acestea numai pe la capete. Aceste capete sunt chiar head şi tail ale unui deque.
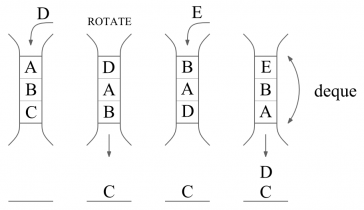
La final, când se vor termina operaţiile, cărţilor de pe raft li se vor adăuga cele din deque şi se va afişa soluţia. În cazul presupus, soluţia va fi: E B A D C.
Întrucât operaţiile unui deque se execută în O(1) amortizat, soluţia are complexitatea O(N + M).
Problema 2: Vila 2 (.campion)
Se dă un şir S de N numere întregi şi un D număr natural. Se cere să determine diferenţa maximă dintre oricare două numere din şir cu proprietatea că diferenţa indicilor nu depăşeşte D.
Restricţii: 2 ≤ N ≤ 100 000, 1 ≤ D ≤ N/2.
Soluţie:
Soluţia nu e greu de intuit. Considerăm indicii succesiv 1, 2, .. , N. Va trebuie ca pentru fiecare secvenţă (i - D, i] să determinăm valoarea maximă şi pe cea minimă, iar diferenţa lor să o comparăm cu rezultatul obţinut până în acel moment. Pentru fixarea ideilor, să urmărim cum putem determina valoarea maximă din fiecare secvenţă (i - D, i].
Observaţie: „Fie i1, i2 doi indici din astfel încât i - D < i1 < i2 ≤ i.
- Dacă S[i1] < S[i2] atunci, cât timp cei doi indici vor fi în intervalul (i - D, i], valoarea de pe poziţia i2 va fi întotdeauna preferată valorii de pe poziţiei i1. Când unul din indici nu va mai fi în acest interval, cel expediat va fi i1 şi, astfel, i2 rămâne în continuare preferat.
- Dacă S[i1] > S[i2] atunci îl vom păstra pe i2, deoarece este candidat la maxim în viitor.”
Cu această observaţie deducem că într-o secvenţă (i - D, i] vom avea un şir i1 < i2 < ... < iK astfel încât S[i1] > S[i2] > ... > S[iK]. Când vom avansa la secvenţa următoare, (i - D + 1, i + 1], vom şterge din indici i1, i2... atâta timp cât nu se găsesc în intervalul curent şi vom şterge din poziţiile iK, iK-1... cât timp S[i + 1] > S[iK], S[i + 1] > S[iK-1]... adică cât timp se îndeplineşte primul punct din observaţia anterioară.
Şirul i1 < i2 < ... < iK este continuu iar operaţiile se efectuează doar pe la cele două capete. Rezultă că şirul poate fi implementat cu ajutorul unui deque.
Pentru S[] = {5, 9, 4, 7, 4, 1} şi D = 3 obţinem următoarele stări ale unui deque:

Cum fiecare indice din 1, 2, .., N trece cel mult o dată prin deque complexitatea finală este O(N) amortizat.
Problema 3: Şir
Se dă un şir S de numere întregi de lungime N. Se cere să se găsească secvenţa de lungime maximă cuprinsă între X şi Y astfel încât MAX - MIN ≤ Z, unde MAX este maximul dintre toate numerele întregi din secvenţă iar MIN minimul dintre acestea. Secvenţa soluţie va fi cea cu poziţia de început maximă dintre toate secvenţele de lungime maximă.
Restricţii: 3 ≤ N ≤ 100 000, 1 ≤ X ≤ Y ≤ N, 0 ≤ Z ≤ 30 000.
Soluţie
Voi prezenta mai jos o rafinare a soluţiei în trei paşi.
Prima rezolvare se găseşte uşor, deoarece nu facem decât să urmărim textul: pentru fiecare poziţie i fixată (i ia valorile 1, 2, .., N succesiv) vom determina pentru aceasta secvenţa cerută, adică vom plimba un j între poziţiile i - Y şi i - X. Pentru un interval (j, i] vom determina MAX şi MIN în O(log2N) cu un arbore de intervale, iar daca diferenţa dintre acestea nu depăşeşte Z vom compara cu soluţia finală. Complexitatea finală va fi O(N * (Y - X) * log2Y).
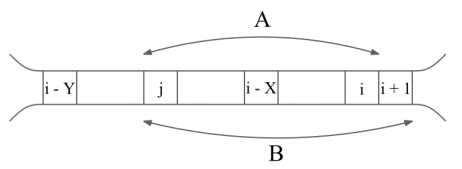
Să presupunem că pentru poziţia curentă i, l-am găsit pe j cuprins între i - Y şi i - X care îndeplineşte optimul. Ce proprietăţi are j?
- i - Y ≤ j ≤ i - X şi MAX - MIN ≤ Z;
- dacă îl incrementăm pe j la j + 1 atunci dacă j ≤ i - X cu siguranţă MAX - MIN ≤ Z şi astfel soluţia va fi mai scurtă;
- dacă îl decrementăm pe j, atunci ori j < i - Y ori MAX - MIN > Z;
- dacă îl incrementăm pe i la i + 1, atunci se poate întâmpla ca j < i - Y; cum MAX nu poate decât să crească, iar MIN decât să scadă, se mai poate de asemenea întâmpla ca MAX - MIN > Z.
Datorită proprietăţilor de mai sus, când trecem de la i la i + 1, valoarea lui j nu poate decât să crească cât timp j < i - Y sau MAX - MIN > Z şi j nu a depăşit poziţia i - X. Pentru determinarea lui MAX, respectiv lui MIN se poate folosi un arbore de intervale. Complexitatea finală va fi O(N * log2(Y)).
Cu cei doi indici i şi j vom accesa fiecare element din cele N de cel mult 2 ori, o dată cu i şi o dată cu j. Să vedem cum putem îmbunătăţi complexitatea O(log2Y) pentru determinarea maximului şi minimului.
Pentru fixarea ideilor să urmărim cum îl calculăm pe MAX. Observaţia care ne ajută în multe probleme pentru reducerea complexităţii de la O(log2N) la O(1) amortizat este următoarea:
Observaţie: „Fixăm i1 şi i2 astfel încât j < i1 < i2 ≤ i. Atunci, dacă S[i2] > S[i1] poziţia i2 va fi întotdeauna mai importantă decât poziţia i1 atâta timp cât cele două poziţii vor fi în intervalul (j, i]. Când i1 şi i2 nu vor mai fi ambele în intervalul (j, i], poziţia eliminată va fi i1. Dacă însă S[i1] > S[i2], atunci poziţia i1 va umbri poziţia i2 atâta timp cât cele două poziţii vor fi în intervalul (j, i]. Când i1 va fi eliminat, atunci e posibil ca i2 să fie un candidat la MAX dintre restul elementelor de la dreapta sa. În acest caz, nu putem afirma nimic şi vom păstra cele două poziţii.”
Rezultă din această observaţie că în intervalul (j, i] poziţiile importante vor fi j < i1 < i2 < .. < ik <= i astfel încât S[i1] > S[i2] > .. > S[ik]. Astfel, MAX va fi S[i1]. Când îl vom incrementa pe i la i + 1 vom şterge din poziţiile ik, ik-1, ... atâta timp cât S[i + 1] este mai important, adică mai mare decât valorile de pe aceste poziţii, şi vom şterge i1, i2, ... atâta timp cât aceste poziţii sunt mai mici sau egale decât j'. Indicele j' este noul optim pentru poziţia i + 1. Proprietatea şirului de poziţii i1, i2, .., ik este că se reprezintă ca un şir continuu de numere care permite inserarea elementelor prin dreapta şi ştergerea prin stânga, adică se adaugă elemente la tail şi se şterg elemente de la head. Îl putem deci reprezenta printr-un deque. Complexitatea O(1) amortizat provine de la faptul că fiecare poziţie dintre cele N nu trece decât o singură dată prin deque şi este şters tot cel mult o singură dată.
În practică, pseudocodul poate arăta în felul următor:
// S şirul de numere iniţial şi N lungimea sa
Subalgoritmul push_in(deque, întreg p, funcţia fct) este:
cât timp (!deque.empty() şi fct(S[p], S[deque.back()])) execută
deque.pop_back();
deque.push_back(p);
Sfârşit;
Funcţia query(deque, întreg j) este:
cât timp (!deque.empty() şi deque.front() <= j) execută
deque.pop_front();
return S[deque.front()];
Sfârşit;
Algoritmul este:
lg = 0;
pentru i = 1, N execută
// funcţia min(a, b) întoarce true dacă a < b
inserează(min_deq, i, min);
// funcţia max(a, b) întoarce true dacă a > b
inserează(max_deq, i, max);
cât timp ((j < i - Y sau query(max_deq, j) - query(min_deq, j) > Z) şi j < i - X) execută
j = j + 1;
// (j, i] este intervalul candidat la soluţia optimă pentru poziţia i
dacă (j <= i - X) şi (query(max_deq, j) - query(min_deq, j) <= Z) atunci
dacă (lg >= i - j) atunci
lg = i - j, start = j + 1, stop = i;
sfârşit_pentru
dacă (lg > 0) atunci
scrie lg, start, stop;
altfel
scrie -1;
Sfârşit.Complexitatea finală va fi O(N).
Problema 4: Trans (ONI 2004)
Se dau N blocuri de piatră, de culoare albă sau neagră aşezate în ordinea 1, 2,.., N. Blocurile de piatră trebuie să fie transportate în ordinea în care sunt, iar pentru aceasta va trebui închiriat un camion. Se mai dau Q tipuri de camioane. Camionul de tipul i (1 ≤ i ≤ Q) poate transporta maxim Ki blocuri de piatră la un moment dat şi pentru un transport se percepe taxa Ti. Se impune condiţia ca toate blocurile de piatră plasate în camion la un transport sa aibă aceeaşi culoare. Aşadar, pentru a fi transportate toate blocurile, se va alege un camion de un anumit tip, iar camionul va efectua unul sau mai multe transporturi. Pentru a micşora suma totală plătită, există posibilitatea de a schimba culoarea oricărui bloc de piatră (din alb în negru sau din negru în alb); pentru fiecare bloc i (1 ≤ i ≤ N) se cunoaşte suma Si ce trebuie plătită pentru a-i schimba culoarea Ci.
Cerinţă: Pentru fiecare dintre cele Q tipuri de camioane, determinaţi suma minimă plătită pentru a transporta toate cele N blocuri.
Restricţii: 1 ≤ N ≤ 16 000, 1 ≤ Q ≤ 100, 1 ≤ Ki ≤ N.
Soluţie:
Soluţia problemei se bazează pe găsirea unei formule de recurenţă ce respectă principiul optimalităţii al metodei programării dinamice.
Pentru început, fixăm un camion dintre cele Q. Fie K numărul maxim de pietre pe care acesta le poate transporta şi T taxa percepută. Notăm sum[i][c] costul pentru a schimba toate pietrele 1, 2, .., i în culoarea c (c = 0 pentru alb şi c = 1 pentru negru). În sum[i][c] se vor aduna toate valorile S[j], cu j ≤ i pentru care C[j] = 1 - c.
În continuare, considerăm bst[i][c] costul minim pentru a transporta pietrele 1, 2, .., i, iar ultimul transport conţine pietre de culoare c. Întrucât nu putem transporta mai mult de K pietre, bst[i][c] depinde doar de poziţiile i - K, i - K + 1, ..., i - 1. Cunoaştem că ultimul camion va transporta o secvenţă continuă de pietre începând de la o poziţie j + 1 până la poziţia i, unde i - K ≤ j ≤ i - 1. Astfel, pentru fiecare j în intervalul precedent, costul va fi Min(bst[j][0], bst[j][1]) (transportăm primele j pietre cât mai ieftin) adunat cu sum[i][c] - sum[j][c] (costul transformării pietrelor j + 1, .., i în culoarea c) şi plus taxa T. Rezultă recurenţa:
- bst[i][c] = Min{ Min(bst[j][0], bst[j][1]) + sum[i][c] - sum[j][c] } + T, unde i - K ≤ j ≤ i - 1.
Dacă ne vom opri aici, complexitatea soluţiei va fi O(Q * N2).
Relaţia de recurenţă poate fi îmbunătăţită. Observăm că pentru poziţia i, sum[i][c] este o valoare constantă, ca şi T. Astfel, deducem următoarea relaţie de recurenţă:
- bst[i][c] = Min{ Min(bst[j][0], bst[j][1]) - sum[j][c] } + sum[i][c] + T, unde i - K ≤ j ≤ i - 1.
Notez în continuare, pentru uşurinţă în scriere, X[j][c] = Min(bst[j][0], bst[j][1]) - sum[j][c]. Să fixăm doi indici i1 şi i2, astfel încât i - K ≤ i1 < i2 ≤ i - 1. Dacă X[i1][c] > X[i2][c] atunci, întotdeauna poziţia i2 va fi preferată poziţiei i1. Când cele două nu se vor mai afla în intervalul [i - K, i - 1], poziţia eliminată va fi poziţia i1. Dacă X[i1][c] < X[i2][c], atunci nu putem decide care poziţie este mai bună în viitor, aşa că le vom păstra pe ambele. Rezultă mai departe că în intervalul [i - K, i - 1] vom avea o serie de indecşi candidaţi la minim i - K ≤ i1 < i2 < .. < in ≤ i - 1 astfel încât X[i1][c] < X[i2][c] < .. < X[in][c]. Mai departe, găsim bst[i][c] ca fiind X[i1][c] + sum[i][c] + T. Urmează să îl introducem şi pe X[i][c], el fiind egal cu Min(bst[i][0], bst[i][1]) - sum[i][c], în şirul de indecşi de mai sus. Acest lucru se va face în felul următor: se vor elimina din in, in-1, ... atâta timp cât X[in][c] > X[i][c], X[in-1][c] > X[i][c], ... adică atâta timp cât poziţia i este preferată lui in, in-1... Fiind la poziţia i + 1, intervalul se va transforma în [i - K + 1, i], aşadar, vom mai elimina din primii indici i1, i2,... atâta timp cât i1 < i - K + 1, i2 < i - K + 1...
După cum am arătat şi la problema precedentă, acest şir de indecşi i1, i2, .., in are proprietatea că este un şir continuu de numere care admite inserări prin dreapta (tail) şi ştergeri prin stânga (head). Şir ce poate fi reprezentat printr-un deque. Cum fiecare index dintre 1, 2, .., N va trece o singură dată prin deque şi va fi şters cel mult o dată, complexitatea soluţiei în acest caz va fi O(Q * N).
În practică, programul este scurt, clar şi foarte eficient:
#include <iostream>
#include <fstream>
#include <vector>
#include <deque>
#include <algorithm>
using namespace std;
const char iname[] = "trans.in";
const char oname[] = "trans.out";
#define MAXN 16005
#define Min(a, b) ((a) < (b) ? (a) : (b))
#define FOR(i, a, b) for (int i = (a); i <= (b); ++ i)
int C[MAXN], S[MAXN], bst[MAXN][2], sum[MAXN][2], N;
void insert(deque < pair <int, int> >& deq, const pair <int, int>& p) {
while (!deq.empty() && deq.back().second > p.second)
deq.pop_back();
deq.push_back(p);
}
int query(deque < pair <int, int> >& deq, const int idx) {
while (deq.front().first < idx)
deq.pop_front();
return deq.front().second;
}
int work(const int K, const int T) {
deque < pair <int, int> > deq[2]; // pair (idx, value)
FOR (c, 0, 1)
insert(deq[c], pair <int, int>(0, 0));
FOR (i, 1, N) { // obiectul i
FOR (c, 0, 1) // culoare
bst[i][c] = query(deq[c], i - K) + sum[i][c] + T;
FOR (c, 0, 1)
insert(deq[c], pair <int, int>(i, Min(bst[i][0], bst[i][1]) - sum[i][c]));
}
return Min(bst[N][0], bst[N][1]);
}
int main(void)
{
ifstream in(iname); ofstream out(oname);
in >> N;
FOR (i, 1, N) {
in >> C[i] >> S[i];
FOR (c, 0, 1)
sum[i][c] += sum[i - 1][c];
sum[i][1 - C[i]] += S[i];
}
int cnt, K, T;
in >> cnt;
FOR (i, 1, cnt)
in >> K >> T, out << work(K, T) << "\n";
in.close(), out.close();
return 0;
}Problema 5: Otilia (.campion)
Otilia şi Burbucel au o grămadă de N pietre şi vor juca un joc cu următoarele trei reguli: 1. Primul jucător are voie să ia din gramadă cel mult K piese; 2. Cu excepţia primei mutări, fiecare jucător are voie să ia maxim P * t pietre, unde t este numărul de pietre care au fost substituite din grămadă la mutarea precedentă; 3. Pierde cel care mută ultimul (cel care ia ultimele pietre din grămadă).
Cerinţă: Se dau M jocuri prin numerele N, K şi P. Se cere să se determină dacă Otilia va câştiga fiecare din jocuri sau nu.
Restricţii: 1 ≤ M ≤ 30 000, 1 ≤ N ≤ 5 000 000, 1 ≤ K ≤ N, 1 ≤ P ≤ 10.
Soluţie:
Problema se rezolvă prin programare dinamică. Soluţia se bazează pe observaţia de mai jos. Considerăm P-ul fixat şi notăm cu stare(X, Y) poziţia de start în care avem X pietre şi numărul maxim de pietre care se pot lua la prima mutare este Y.
Observaţia 1: „Dacă există strategie sigură de câştig pentru stare(X, Y) atunci există şi pentru orice stare(X, T) cu T ≥ Y.”
De ce? Pentru că orice mutare validă pentru stare(X, Y) este validă şi pentru stare(X, T). Având această observaţie notăm cu MinY[X] = Y, Y minim astfel încât avem strategie de câştig pentru stare(X, Y).
Observaţia 2: „stare(X, Y) este pierzătoare dacă şi numai dacă Y < MinY[X].”
Aceasta reiese din definiţia lui MinY[X].
MinY[X] se calculează după următoarea recurenţă, care rezultă din regulile jocului:
- MinY[X] este cel mai mic i pentru care avem MinY[X - i] > P * i.
De aici se naşte prima soluţie, care este implementarea directă a recurenţei. Deşi complexitatea acesteia pare a fi O(N2) ea se comportă foarte bine pentru N ≤ 500 000. Aşadar, această soluţie acoperă aproximativ 50% din testele de intrare. Printr-o rafinare a acestei soluţii se obţine un algoritm de complexitate O(N). Rafinarea se bazează pe:
Observaţia 3: „Să presupunem că dorim să calculăm MinY[X]. Facem următoarea afirmaţie: orice poziţie rea pentru X (în care dacă mutăm pierdem) va fi rea şi pentru X + 1.”
Acest lucru este simplu de observat dacă privim ce înseamnă că o poziţie Q e rea pentru X:
- MinY[Q] > X - Q, pentru X;
- MinY[Q] > X - Q + 1, pentru X + 1.
Este evident că prima relaţie o implică pe cea de-a doua. În momentul acesta se poate construi următorul algoritm: având lista de poziţii care pot fi bune pentru X (sortată descrescător) o căutăm pe cea mai mare ca valoare care este într-adevăr bună. În principiu, scoatem din capul listei poziţiile rele până când dăm de o poziţie bună. La listă se va adăuga şi X şi se va trece la pasul următor. Operaţiile algoritmului sunt chiar operaţiile asupra unui deque.
Problema 6: Bcrc (Stelele Informaticii 2006)
Se consideră N camere, numerotate de la 1 la N, aşezate în cerc. Iniţial (la momentul de timp 0), ne aflăm în camera 1. În fiecare moment de timp, putem alege să rămânem în camera în care ne aflăm sau să ne deplasăm într-o cameră vecină într-o unitate de timp. Se dă o listă de M cutii ce conţin bomboane prin T, C şi B: cutia apare la momentul T în camera C şi conţine B bomboane. Cutia va dispărea la momentul T + 1.
Cerinţă: Cunoscând numărul de camere din labirint şi momentele de timp la care apar cutiile cu bomboane, determinaţi care este numărul maxim de bomboane pe care le putem culege.
Restricţii: 3 ≤ N ≤ 2 048, 0 ≤ M ≤ 50 000, 1 ≤ T ≤ 1 000 000 000, 1 ≤ C ≤ N, 1 ≤ B ≤ 9 999.
Soluţie:
Soluţia foloseşte metoda programării dinamice.
O stare se reprezintă prin camera în care ne aflăm şi momentul de timp. Fie bst[i][j] numărul maxim de bomboane culese până în momentul i când ne găsim în camera j. O observaţie evidentă este că bst[i][j] se poate modifica doar în momentele în care apar cutiile. Prin urmare, vom considera momentele de timp când apar cutiile, momente ce sunt în număr de M, bst[i][j] însemnând numărul maxim de bomboane culese ştiind că ne aflăm în camera j unde am cules cutia i. De cine depinde această stare? Ştim că bst[i - 1][1 ... N] a fost deja calculat în mod optim. Să notăm cu T diferenţa de timp dintre momentele la care apare cutia i şi cutia i - 1. În acest moment i şi cameră j putem ajunge din maxim T camere spre stânga sau spre dreapta, întrucât fiecare deplasare între două camere costă o unitate de timp. De unde deducem că:
- bst[i][j] = Min { bst[i - 1][j - T], bst[i - 1][j - T + 1], ..., bst[i - 1][j], ..., bst[i - 1][j + T - 1], bst[i - 1][j + T] }.
Metoda directă şi, aparent eficientă, constă în folosirea unui arbore de intervale pentru aflarea acestui minim. Însă, intervalul se deplasează, dacă vom considera indicii j în ordine 1, 2, 3, ... constant spre dreapta, fiind reprezentat de un şir de valori de lungime constantă în care noile elemente se introduc prin dreapta şi altele se elimină prin stânga. Vom folosi un deque de lungime 2 * T şi vom proceda ca în problemele precedente, eliminând poziţiile care nu sunt candidate la soluţie. Mai jos este o reprezentare grafică a acestei explicaţii.
Complexitatea finală: O(M * N).
Problema 7: Cut the Sequence (PKU)
Se dă o secvenţă S de numere întregi de lungime N. Va trebui să se împartă secvenţa în mai multe subsecvenţe astfel încât suma valorilor din fiecare parte să nu depăşească un număr întreg M dat, iar dacă însumăm maximul din fiecare subsecvenţă să obţinem o sumă cât mai mică.
Restricţii: 0 < N ≤ 100 000, 0 ≤ Si ≤ 1 000 000.
Soluţie:
Voi face un desen pentru explicaţii. :)
Algoritmul este:
// S[] şirul iniţial de numere iar N lungimea sa
// (last, i] este intervalul de lungime maximă care se termină în i a cărui sumă nu depăşeşte M
sum = 0;
last = 0;
// indicii head si tail ai dequeului
deque[head = tail = 1] = 0;
pentru i = 1, N execută
sum += S[i];
temp = bst[ deque[tail] ];
cât timp (head <= tail) şi S[ deque[tail] ] <= S[i] execută
temp = Min(temp, iMin[tail]);
tail --;
sfcâttimp
// adaug poziţia i la deque
tail ++;
deque[tail] = i;
// actualizez iMin[]
iMin[tail] = temp;
// actualizez T[]
update(T, tail, iMin[tail] + S[i]);
cât timp (head <= tail) şi (sum > M) execută
sum -= S[last];
dacă (deque[head] == last) atunci
head ++;
sfdacă
last ++;
sfcâttimp
// actualizez iMin[]
iMin[head] = query(bst, last - 1, deque[head] - 1);
// actualizez T[]
update(T, head, iMin[head] + S[ deque[head] ]);
// reţin optimul pentru poziţia curentă
bst[i] = query(T, head, tail);
sfpentru
scrie bst[N];
Sfârşit.Concluzii
Filozofia din spatele structurii de deque devine utilă, de obicei, în părţile finale ale rezolvării unei probleme. Însă, ce pot spune cu certitudine este că această structură de date pe cât este de simplă pe atât este de eficientă.
Probleme suplimentare
Înţelegerea profundă a acestei structuri simple nu se poate realiza decât prin rezolvarea a cât mai multe probleme. Succes!
- Deque, Arhiva educaţională
- Secvenţă
- Secvenţă 3
- Secvenţă 4
- Vila 2, .campion
- Sum 2, Stelele Informaticii 2003
- Drept 2, Lotul Naţional de Informatică, 2006
- Copaci 2, .campion
- Brânză
- Struţi
- Trompetă
- Buline
- Balans
- Gard, ONI 2002
- Ghiozdan
- Munte4, Lotul Naţional de Informatică, 2005
- Cover, ONI 2007, Baraj
Bibliografie
- Cosmin Negruşeri, Probleme cu secvenţe
- Dana Lica, Arbori de intervale şi aplicaţii în geometria computaţională
- C++ Reference, deque
