Rezolvare pentru "suma in triunghi" si functii convexe
Rezolvarea pe scurt:
Functia 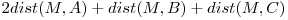 e o functie convexa. Functiile convexe isi ating maximul pe marginea domeniului de definitie. Astfel e de ajuns sa evaluam functia in punctele A, B si C si gasim ca maximul este 13 si e realizat in punctul C.
e o functie convexa. Functiile convexe isi ating maximul pe marginea domeniului de definitie. Astfel e de ajuns sa evaluam functia in punctele A, B si C si gasim ca maximul este 13 si e realizat in punctul C.
Functii convexe:
Problema este pretext pentru a discuta notiunea de functie convexa. O astfel de functie are proprietatea ca pentru oricare doua puncte de pe graficul ei, graficul se afla sub segmentul determinat de cele puncte. Mai formal, daca 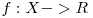 unde
unde 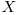 e un domeniu convex (interval etc.) atunci pentru oricare doua puncte
e un domeniu convex (interval etc.) atunci pentru oricare doua puncte 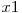 si
si 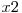 din
din 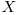 si orice
si orice 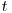 din intervalul
din intervalul ![[0, 1] [0, 1]](https://www.infoarena.ro/static/images/latex/264884439b70ab09a86bc848421c6de6_3.5pt.gif) avem ca
avem ca 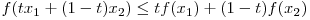 .
. 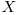 poate fi orice spatiu vectorial, R, interval in o dimensiune, poligon convex in doua si asa mai departe.
poate fi orice spatiu vectorial, R, interval in o dimensiune, poligon convex in doua si asa mai departe.
O proprietate importanta a functiilor convexe este ca au doar un minim local care este si global. Astfel problema minimizarii valorii unei functii multi dimensionale este mai simplu de rezolvat pentru functii convexe. Ea apare frecvent in machine learning. Functiile generale nu sunt usor de minimizat. Nu au o forma care poate fi rezolvata matematic sau sunt neregulate si au multe optime locale. Pentru a putea obtine solutii bune, de multe ori functiile generale sunt aproximate de functii convexe pentru care exista algoritmi eficienti de minimizare, cum ar fi cautare ternara pentru cazul unidimensional sau gradient descent pentru cazul general.
Rezolvarea mai detaliata:
Functia distanta euclidiana fata de un punct fix e o functie convexa.
demonstratie:
Vedem usor daca facem un grafic care este un con sau putem incerca sa ne uitam la derivate.
Suma a doua functii convexe este tot o functie convexa.
demonstratie:
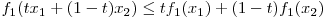
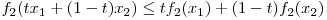
=>
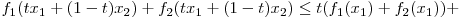
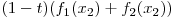
Astfel 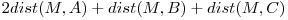 e si ea o functie convexa.
e si ea o functie convexa.
 Maximul pentru o functie convexa e realizat pe marginea domeniului de definitie.
Maximul pentru o functie convexa e realizat pe marginea domeniului de definitie.
demonstratie:
Din definitie, graficul intre 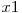 si
si 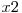 se afla sub segmentul determinat de
se afla sub segmentul determinat de 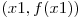 si
si 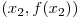 astfel pentru
astfel pentru 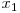 si
si 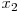 pe contur unul dintre cele doua puncte va fi mai sus decat toate restul din grafic.
pe contur unul dintre cele doua puncte va fi mai sus decat toate restul din grafic.
Acum am demonstrat toti pasii din prima propozitie a articolului.
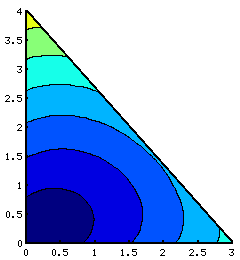
In graficul alaturat puteti vedea cum se comporta functia. Punctele A, B si C au coordonatele (0, 0), (3, 0) respectiv (0, 4), iar culoarea graficului reprezinta suma ceruta in problema.
Aveti aici codul in Octave cu care e generat.dist = @(x, y, x1, y1) sqrt((x - x1).^2 + (y - y1).^2)
sumt = @(x, y) 2 * dist(x, y, 0, 0) + dist(x, y, 3, 0) + dist(x, y, 0, 4)
x = linspace(0, 3, 50)
y = linspace(0, 4, 50)
[xx, yy] = meshgrid(x, y)
contourf(xx, yy, sumt(xx, yy))Cerinta de gasire a maximului e putin fortata pentru a face problema posibil de rezolvat in cap. Pentru ca in general la functii convexe cautam minimul. Putem avea maxime locale in orice colt al frontierei, deci pentru o frontiera cu multe colturi nu avem algoritmi eficienti.
Adapost2 se poate rezolva folosind idei din acest post.
Sper ca v-am deschis apetitul pentru functii convexe :).
