Solutia problemei Dupadealuri

Multumim lui Donciu Mircea •Mircea_Donciu pentru editorial!

Solutie O(N^3) – 20 de puncte

Pentru orice subsecventa din sir, eliminam acea subsecventa si apoi verificam daca ce ne-a ramas este un palindrom. Complexitate .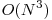

Solutie O(N^2) – 40 de puncte

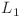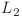Orice palindrom posibil va arata ca in imaginea de mai sus, cu secventele si (posibil vide) de lungime egala si simetrice si cu palindromul P. Prin urmare o solutie ar fi sa mergem cu un iterator l de la 0 la n/2 care sa ne dea lungimea 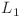si 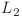, verificand ca prefixul rescpectiv sufixul de lungime l sunt simetrice. Pentru fiecare l valid putem gasi toate palindroamele P care se invechineaza cu l in 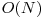pentru fiecare l cu hashing sau cu Algoritmul lui Manacher. Complexitate totala .

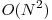Solutie O(N) – 100 de puncte.

Solutia de 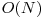e foarte similara cu cea de 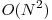numai ca incercand pentru fiecare l sa aflam rezultatul in 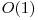. Facand mai intai Manacher pe tot sirul putem afla pentru fiecare punct i palindromul maximal din i ($nota:$ la Manacher i nu e neaparat un numar natural datorita palindroamelor de lungime para).
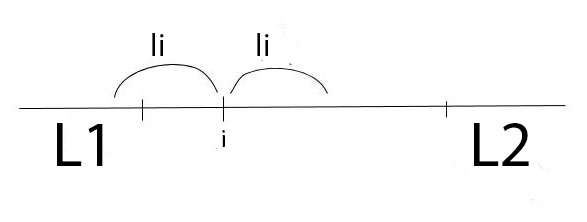
Dupa cum se vede mai jos 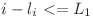si 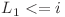daca si numai daca va exista un palindrom cu centrul in i care sa se invechineze cu 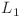. Dat fiind ca lungimile lui 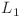, 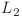care se invechineaza cu un palindrom cu centrul in i, sunt consecutive si stiut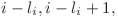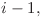e (… unde 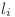este distanta de la i la capatul palindromului maximal) putem face Mo pentru a afla raspunsul final.

Nota de final: Aveti grija pentru fiecare i la cine faceti suma partiala in functie de care dintre 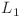si 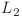va invechina palindromul cu centrul in i.