Solutia problemei Djok

Multumim lui georgerapeanuRapeanu George •georgerapeanu pentru editorial!

Solutie 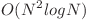O(N^2logN) - 30p

Sa zicem ca Tanaka alege sa controleze monstruletul din nodul i. Atunci o strategie optima pentru el este sa atace tot timpul cel mai slab monstrulet din nodurile nevizitate in care poate ajunge. Strategia aceasta este optima pentru ca fie Tanaka poate bate monstruletul, caz in care vitejia monstrului controlat fie creste fie ramane la fel, fie nu il poate bate, dar atunci el nu va putea bate niciun alt monstrulet la care are acces. Asadar problema ne cere ca, pentru o multime de noduri vizitate, sa gasim nodul adiacent unuia dintre nodurile deja vizitate, care contine monstruletul cu cea mai mica vitejie. Asadar, pentru un nod de inceput i fixat, putem sa il bagam intr-un heap. Acum vom face un algoritm asemanator celui de BFS/Dijkstra, si vom tot extrage din heap nodul cu cel mai mic cost, vom verifica daca putem bate monstruletul din nodul acela, si daca da il scoatem si ii adaugam in heap vecinii nevizitati, si eventual actualizam vitejia monstruletului nostru.

Solutie 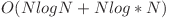O(NlogN + Nlog*N) - 100p

Fie 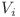V_i vitejia monstruletului din nodul i.
Fie 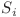S_i multimea nodurilor la care poti ajunge din i si pe care le poti bate cu monstruletul din nodul i fara a iti schimba vitejia.
Atunci 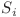S_i va fi multimea conexa de noduri cu valori pana in 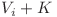V_i + K , care il contine pe i.
Se poate observa ca daca in multimea asta exista un nod j, cu vitejia mai mare decat i, atunci 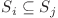S_i \subseteq S_j . De ce?
Deoarece j se afla in 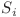S_i , inseamna ca pe lantul de i la j toti monstruletii au vitejia mai mica sau egala cu 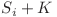S_i + K, si cum 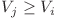V_j \geq V_i , sigur putem ajunge si din nodul j in nodul i, si deci acum e ca si cum am porni cu un monstrulet cu vitejia 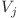V_j din nodul i, ceea ce e mai bine. Deoarece 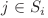j \in S_i , inseamna ca putem sa batem monstruletul j, deci putem creste vitejia monstruletului nostru la 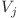V_j . Asadar, raspunsul pentru nodul i va fi acelasi cu raspunsul pentru nodul j.

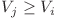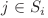Acum ce mai ramane de vazut e cum gasim pentru un nod i, un nod j cu V_j \geq V_i cu j \in S_i . Pentru asta vom pune intrebarea invers: un nod i, pentru ce alte noduri este nodul cautat? Hai sa sortam nodurile crescator dupa 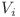V_i . Cum am mentionat anterior, toate 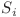S_i sunt multimi conexe de noduri, si asta ne-ar putea face sa ne gandim la paduri de multimi disjuncte. Hai sa inseram nodurile arborelui crescator dupa valoare. Sa zicem ca am inserat primele i - 1 noduri,si acum suntem la al i-lea. Vom creea o noua multime pentru nodul nod inserat si vom uni cu aceasta toate multimile care contin un nod vecin al nodului nou inserat. Nodul curent va putea fi nodul cautat doar pentru nodurile cu vitejie maxima din aceste multimi. De ce? Pentru ca orice alt nod din ele au avut deja oportunitatea de a se lega de nodul cu vitejie maxima din multimea lor, deci daca nu au facut-o e pentru ca au vitejia prea mica pentru acesta. Asadar, la unirea unei multimi cu noua multime a nodului al i-lea, vom verifica daca nu cumva nodul cu vitejia maxima din ele nu poate sa se lege de nodul curent.

Acum stim pentru fiecare nod i, fie stim un nod j care are acelasi raspuns, fie un nod de genul nu exista, ceea ce ar inseamna ca monstruletul din nodul i nu isi va schimba niciodata vitejia, si asadar va bate doar noduri la care poate ajunge fara sa isi schimbe vitejia, adica 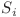S_i . O ultima observatie ne ajuta sa finalizam problema: multimea 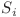S_i este egala cu multimea care contine nodul i, de la momentul in care in structura de paduri de multimi disjuncte de la pasul anterior l-am inserat pe i. Asadar, putem tine minte aceasta dimensiune, iar la final pentru a afla raspunsul pentru i sa folosim o structura asemanatoare multimiilor de paduri disjuncte.

O solutie bazata pe aceasta idee se gaseste aici