Solutia problemei Bisuma

Multumim lui TincaMateiTinca Matei •TincaMatei pentru editorial!

Solutie O(N2 * K) - 30 de puncte

Vom rezolva aceasta problema folosind programarea dinamica. Fie dinamica:
dp[K][N] = \mbox{valoarea minima a impartirii daca as folosi K bucati folosind primii N copii}

Formula de recurenta este urmatoarea:
dp[K][N] = min(dp[K][T] + max(a[T + 1] + a[T + 2] + ... + a[N], b[T + 1] + b[T + 2] + ... + b[N]))

Pentru a simplifica formula, vom folosi sume partiale: sa[N] = a[1] + a[2] + ... + a[N] si sb[N] = b[1] + b[2] + ... + b[N] . Astfel formula va deveni:

dp[K][N] = min(dp[K - 1][T] + max(sa[N] - sa[T], sb[N] - sb[T]))

Formula de recurenta are complexitatea O(N), astfel complexitatea finala va deveni O(N2 * K).

Solutie O(N * K * logN) - 100 de puncte

Pentru a rezolva problema, trebuie sa analizam si mai mult formula de recurenta. Pentru inceput, vom explicita functia de maxim din interior:
dp[K][N] = min \begin{cases} dp[K - 1][T] + sa[N] - sa[T], & \mbox{daca } sa[N] - sa[T] >= sb[N] - sb[T] \ dp[K - 1][T] + sb[N] - sb[T], & \mbox{in caz contrar contrar} \end{cases}

Rescriind conditia pentru primul caz, obtinem
dp[K][N] = min \begin{cases} dp[K - 1][T] + sa[N] - sa[T], & \mbox{daca } sa[N] - sb[N] >= sa[T] - sb[T] \ dp[K - 1][T] + sb[N] - sb[T], & \mbox{in caz contrar contrar} \end{cases}

Grupand termenii, mutandu-i in fata, obtinem
dp[K][N] = min \begin{cases} sa[N] + min(dp[K - 1][T] - sa[T]), & \mbox{daca } sa[N] - sb[N] >= sa[T] - sb[T] \ sb[N] + min(dp[K - 1][T] - sb[T]), & \mbox{in caz contrar contrar} \end{cases}

Pentru a calcula dinamica, vom folosi doi vectori auxiliari initializati cu infinit pe toate pozitiile, fie acestia besta si bestb. Cand calculam dp[K][N], vrem ca besta[x] = min(dp[K][T] - sa[T] unde T < N si sa[T] - sb[T] == x), analog pentru bestb. Astfel, formula va deveni:
dp[K][N] = min \begin{cases} sa[N] + min(besta[T] \mbox{ pentru } T <= sa[N] - sb[N]) \ sb[N] + min(bestb[T] \mbox{ pentru } T >= sa[N] - sb[N])\end{cases}

Aceasta structura de date este ineficienta, deoarece, desi update-ul se face in O(1), query-ul se face in complexitate O(VAL_MAX). Pentru a optimiza aceasta structura, putem folosi una din urmatoarele structuri:

  • un arbore de intervale in care normalizam coordonatele sa[T] - sb[T] cu O(logN) per update sau query
  • un arbore indexat binar in care normalizam coordonatele sa[T] - sb[T] cu O(logN) per update sau query
  • un set in care atunci cand inseram o pereche {sa[N] - sb[N], dp[K][N] - sa[N]}, eliminam toate perechile {x, y} cu sa[N] - sb[N] ≥ x si dp[K][N] - sa[N] ≤ y cu O(logN) per update sau query
  • un arbore binar echilibrat cu O(logN) per update sau query
  • un arbore de intervale alocat dinamic cu O(logVAL_MAX) per update sau query

Interpretare geometrica

Sa ne intoarcem la formula de recurenta de mai devreme:
dp[K][N] = min(dp[K - 1][T] + max(sa[N] - sa[T], sb[N] - sb[T]))

Putem observa ca max(sa[N] - sa[T], sb[N] - sb[T]) = max(|sa[N] - sa[T]|, |sb[N] - sb[T]|). Aceasta formula reprezinta distanta Cebisev intre punctele {sa[N], sb[N]} si {sa[T], sb[T]}. Astfel, putem sa consideram in plan punctele {sa[N], sb[N]}.

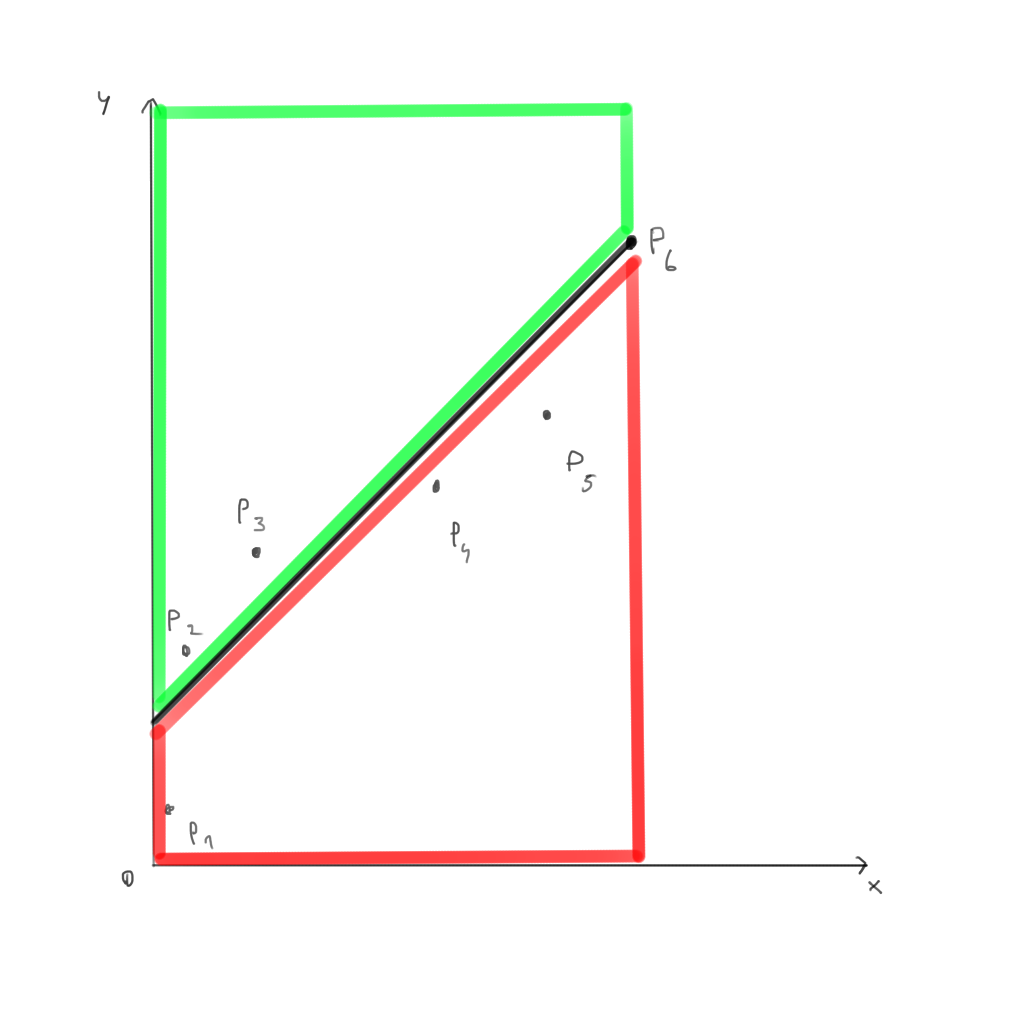
Sa presupunem ca pentru un anumit K, vrem sa calculam dp[K][6] pe desenul de mai sus. Putem observa ca in semiplanul marcat cu rosu, distanta Cebisev intre P6 si orice alt punct din in planul rosu va fi diferenta absoluta pe proiectiile celor doua puncte pe axa Oy, iar in cele din planul marcat cu verde va fi diferenta absoluta pe proiectiile celor doua puncte pe axa Ox. O sa tinem minte pentru fiecare diagonala paralela cu diagonala x = y care este dp[K][T] - sa[T] minim, respectiv dp[K][T] - sb[T]. Pentru un punct {x, y}, toate diagonalele se vor imparti in doua clase: cele de deasupra diagonalei din {x, y} si cele de sub diagonala. Pentru cele de deasupra diagonale (de exemplu pe cele din aria verde pentru punctul P6), optimul va fi minimul de pe fiecare diagonala de deasupra la care adunam x. Pentru cele de sub diagonala (cele din aria rosie pentru punctul P6), optimul va fi minimul de pe fiecare diagonala de sub la care adunam y.

Putem numerota diagonalele in mai multe feluri, unul din acestea fiind urmatorul: punctul {x, y} apartine diagonalei d = x - y. Astfel, punctele de sub o diagonala d vor diagonalele d + 1, d + 2, ..., iar cele de deasupra diagonalei d vor fi d - 1, d - 2, ....

Inlocuind modificarile noastre cu datele din solutia precedenta, vom obtine urmatoarele lucruri:

  • Avem punctele {sa[N], sb[N]}
  • Un punct {sa[N], sb[N]} apartine diagonalei d = sa[N] - sb[N]
  • Un punct {sa[T], sb[T]} este deasupra diagonalei d = sa[N] - sb[N] <=> sa[T] - sb[T] <= sa[N] - sb[N]
  • Pentru fiecare diagonala tinem minte dp[K][N] - sa[N] minim, respectiv dp[K][N] - sb[N] minim.

Putem observa echivalenta intre cele doua solutii, punctele 2 si 3 reprezentand conditia din formula de recurenta de mai sus, iar minimele pe care le tinem pentru fiecare diagonala d, vor fi defapt besta[d] si bestb[d], folosind notatiile din solutia precedenta.