Solutii Algoritmiada 2012, Runda 4
Go2
O primă soluţie ar fi să asociem fiecărei celule o variabilă, iar pentru fiecare celulă să scriem ecuaţia specifică: 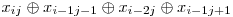 . În final va rezulta un sistem cu MxN ecaţii şi MxN necunoscute. Complexitatea este
. În final va rezulta un sistem cu MxN ecaţii şi MxN necunoscute. Complexitatea este 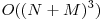 şi obţine 50 de puncte. Pentru a obţine 100 de puncte este necesar să observăm că dacă am fixat prima linie, a doua va fi unic determinată de ea. Aplicând acelaşi raţionament observăm că toata matricea poate fi calculată în funcţie de prima linie.
şi obţine 50 de puncte. Pentru a obţine 100 de puncte este necesar să observăm că dacă am fixat prima linie, a doua va fi unic determinată de ea. Aplicând acelaşi raţionament observăm că toata matricea poate fi calculată în funcţie de prima linie.
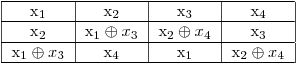
Astfel înlocuind variabilele cu cele corespunzătoare de pe prima linie rămânem cu un sistem cu M variabile şi MxN ecuaţii. În final complexitatea va fi 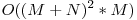
Margele
Solutie O(2N * N * K)
Solutia naiva care genereaza toate configuratiile posibile de lungime N si apoi verifica daca sunt valide obtine 20 de puncte.
Solutie O(22K * (N + K))
Faptul ca K <= 10 si ca rezultatul trebuie afisat modulo 666013 ne sugereaza ca problema se rezolva folosind programare dinamica pe stari exponentiale (deci sunt necesare operatii pe biti). Margelele pot fi vopsite in cel mult doua culori, deci putem reprezenta o subsecventa de K perle printr-un sir binar de lungime K. Vom reprezenta o stare printr-o pereche (p, conf), unde p este pozitia la care ne aflam in colier iar conf este un sir binar de lungime K care reprezinta configuratia de culori a perlelor din intervalul [p - K + 1, p] (bitul 0 va reprezenta culoarea pozitiei p).
Colierul este circular, deci pozitiile din colier au aceasta succesiune 1, 2, ... , N, 1, 2, ... . O mare parte din dificultatea problemei o reprezinta faptul ca trebuie sa luam in considerare si subsecventele care ajung la capatul sirului (pozitia N) si continua la inceput (pozitia 1). Observam ca pe masura ce avansam pozitia p, pierdem informatia despre cum e configuratia colierului la inceput, deoarece tinem informatia doar pentru ultimele K pozitii. Solutia este sa fixam configuratia primelor K perle si astfel cand ajungem la capatul sirului putem verifica daca configuratia curenta este in totalitate valida.
Daca ne aflam pe pozitia p cu configuratia conf atunci avem doar 2 optiuni pentru pozitia p + 1: fie punem 0, fie 1. Configuratia pentru pozitia p + 1 o obtinem shiftand conf la stanga cu o unitate (deoarece acum privim din perspectiva pozitiei p + 1) si adaugarea optiunii la bitul 0. Deoarece gestionam tot timpul ultimele K perle, vom incepe recurenta de pe pozitia K. Cazul de baza este starea ( K, confSt ), unde confSt reprezinta configuratia de start fixata. Vom precalcula toate configuratiile valide de lungime K si le vom folosi doar pe acestea, neavand sens sa le consideram pe restul. Aceasta solutie obtine punctaj maxim.
Fragment de cod:
// precalculez toate configuratiile valide in bconf[] si le memorez de la 1 la bconf[0]
// daca conf e valida atunci bvalid[conf] = 1
if(A == 0) {
bconf[++bconf[0]] = 0;
bvalid[0] = 1;
}
for(conf = 1; conf < (1 << K); conf++) {
bcount[conf] += bcount[conf & (conf - 1)] + 1;
if(A <= bcount[conf] && bcount[conf] <= B) {
bconf[++bconf[0]] = conf;
bvalid[conf] = 1;
}
}
// fixez configuratia de start
for(i = 1; i <= bconf[0]; i++) {
confSt = bconf[i];
memset(dp, 0, sizeof(dp));
// cazul de baza
dp[K][confSt] = 1;
for(p = K; p < N; p++) {
// configuratia curenta
for(j = 1; j <= bconf[0]; j++) {
conf = bconf[j];
if(dp[p][conf] == 0) continue;
// aleg sa pun 0 la p + 1
nconf = (conf << 1) & ((1 << K) - 1);
dp[p + 1][nconf] += dp[p][conf];
if(dp[p + 1][nconf] >= MOD) dp[p + 1][nconf] -= MOD;
// aleg sa pun 1 la p + 1
nconf = (conf << 1) & ((1 << K) - 1) | 1;
dp[p + 1][nconf] += dp[p][conf];
if(dp[p + 1][nconf] >= MOD) dp[p + 1][nconf] -= MOD;
// nu conteaza daca nconf nu e configuratie valida pentru ca
// daca nu e atunci oricum nu ne vom folosi de acea informatie
}
}
// verific care dintre configuratiile valide de la sfarsit se potrivesc cu cea de la inceput
for(j = 1; j <= bconf[0]; j++) {
conf = bconf[j];
// concatenez sfarsitul cu inceputul
conc = (conf << K) | confSt;
ok = 1;
for(k = 1; k < K; k++) {
// retin doar subsecventa care ma intereseaza
nconf = (conc >> k) & ((1 << K) - 1);
if(!bvalid[nconf])
ok = 0;
}
// daca e valida o adaug la rezultat
if(ok) {
rez += dp[N][conf];
if(rez >= MOD) rez -= MOD;
}
}
}Muncitori
La aceasta problema se pot folosi oricare dintre solutiile mentionate la problema Proc2 , cu urmatoarea precizare : acolo taskurile sunt executate de procesoarele 1...M iar aici loturilor li se vor asocia intotdeuna muncitori din intervalul K...N. Pentru implementarea cu usurinta a ideilor mentionate in articolul de mai sus se poate translata intervalul K...N in intervalul 1,N - K + 1 iar la afisare rezultatul se va aduna cu K - 1.
Comentarii suplimentare:
Solutie O(M * N + M * logM)
Sortam muncile dupa timpul de incepere a verificarii. Le parcurgem in ordinea cronologica si pentru fiecare dintre ele cautam secvential al K-lea muncitor liber. O astfel de abordare obtine 20 de puncte.
Solutie O(M * logN + M * logM)
Pentru gasirea in mod eficient a celui de al K-lea muncitor disponibil putem folosi un arbore de intervale. Fiecare nod va contine numarul de muncitori liberi la momentul respectiv pe intervalul asociat lui. Observam ca pe masura ce avansam in timp unii muncitori vor deveni in mod repetat liberi sau ocupati si de fiecare data va trebui sa updatam arborele de intervale. De aceea, retinem intr-un minheap (sau priority_queue sau set) momentul cand muncitorii ocupati vor deveni disponibili. La fiecare moment de timp extragem muncitorii care au devenit liberi si facem update in arborele de intervale. Aceasta abordare obtine 100 de puncte.
Fragment de cod:
// sortam muncile dupa timpul de incepere al verificarii
sort(lot.begin(), lot.end());
// initializam arborele de intervale
init(1, 1, N);
for(i = 0; i < M; i++) {
// cat timp exista in heap un muncitor care a devenit liber intre timp
while(!Q.empty() && Q.top().timp <= lot[i].start) {
// facem update in arbore (marcam muncitorul ca fiind disponibil)
update(1, 1, N);
// scoatem muncitorul din heap
Q.pop();
}
// gasim al K-lea muncitor disponibil
q = query(1, 1, N);
// ii asociem lotul i muncitorului q
asociat[i] = q;
// retinem cand muncitorul q va fi disponibil din nou
tfree[q] = lot[i].start + lot[i].durata;
// facem update in arbore (marcam muncitorul ca fiind ocupat)
update(1, 1, N);
// introducem muncitorul in heap
Q.push(make_pair(tfree[q], q));
}Exista si alte solutii care obtin de asemenea punctaj maxim. De exemplu, putem gasi al K-lea muncitor disponibil folosind un arbore indexat binar si cautarea binara. O alta idee se bazeaza pe observatia ca vom folosi doar muncitorii din intervalul [K, N]. Deci, putem folosi doua minheapuri, unul in care retinem momentul in care vor deveni muncitorii disponibili si altul in care retinem indicii muncitorilor disponibili.
Puteri3
Cu toate ca nu este o explicatie clasica si clara pentru articolul cu solutii, pana cineva va posta solutia oficiala, cei interesati pot citi aceste doua topicuri 1 si 2 .
O solutie naiva, in complexitate O(N*log N), folosind exponentiere logaritmica, obtine 20 de punte.
Spirala3
O prima solutie, care obtine 40 de puncte, presupune gasirea pentru fiecare element de '0' a lungimii celei mai mari spirale care incepe din el.
