Solutii Algoritmiada 2010, Runda 2
- Lista de probleme
- Popularitate
- Dinti
- Secv9
- Redu
- Jap2
- Recurenta2
- Palmieri
Popularitate
Prima varianta pentru rezolvarea acestei probleme este folosirea numerelor mari. Inmultim in prima faza toate numerele dintr-un grup si apoi le impartim la K atata timp cat restul impartirii este 0. Aceasta abordare obtine 30 de puncte.
Atunci cand K este prim, este de ajuns sa calculam puterea la care apare K in fiecare numar al grupului, fie acesta Tj. Atunci popularitatea grupului este P = T1 + T2 + ... + TNi. Aceasta abordare obtine 30 de puncte.
Un program care pentru K compus calculeaza P folosind prima metoda si pentru K prim calculeaza P folosind metoda a doua obtine 50 de puncte.
Solutia de 100 de puncte a problemei se bazeaza pe reducerea cazului in care K este compus la o varianta modificata a rezolvarii pentru K prim. Fie K = K1F1 * K2F2 * ... * KQFQ unde K1, K2 ... KQ sunt factori primi distincti si presupunem ca F1, F2 ... FQ > 0, In acest caz Q < log(K). Fie Pi popularitatea grupului calculata pentru Ki, atunci popularitatea grupului pentru K este min( [Pi / Fi] ) cu 1 ≤ i ≤ Q. Complexitatea finala este O(sqrt(K) + M*N*log(K)).
Dinti
Fie inv(s) inversul sirului s (spre exemplu: inv(100) = 011). Fie S un sir determinat de L caractere consecutive din sirul A. Putem observa ca inv(S) si orice alt sir obtinut din inv(S) prin modificarea oricator valori 1 din inv(S) in 0 se potriveste peste S (exemplu: peste S = 100 se potrivesc 011, 001, 010, si 000).
Numarul total de siruri ce se pot potrivi peste A nu depaseste 2L asa ca putem tine un vector V, de valori adevarat/fals de marime 2L,
astfel incat V[cod(s)] = 1/0 daca sirul s se poate suprapune peste sirul A ( cod(s) reprezinta codificarea sirului s intr-un numar in baza 10 a carei reprezentare binara este egala cu sirul s). Ca sa obtinem acest vector putem lua pe rand toate sirurile S, parcurgand sirul A si tinand ultimele L caractere, si printr-un backtracking sa obtinem toate valorile ce se pot potrivi peste S (calculam inv(S) si apoi schimbam prin backtracking 1-urile in 0-uri in toate modurile posibile). Aceste siruri "bune" le putem stoca in sirul V si apoi putem raspunde la oricare intrebare in O(1). Singura problema este ca aceasta solutie are o complexitate prea mare (cam 3L) si iese din timp. Pentru a nu folosi backtracking in generarea sirurilor bune vom face urmatorul lucru. Pentru toate sirurile S vom tine ca sir bun in V doar inv(S), iar dupa aceea vom folosi o dinamica pentru a afla toate sirurile bune. Pentru toate starile st, de la 2L-1 la 0 (de la 11..1 la 00..0) putem zice ca daca V[st] = 1 atunci si V[st ^ (1 << k)] = 1, pentru toate k-urile pentru care st & (1 << k) != 0 (adica pentru toti bitii de 1 din st). Aceasta dinamica este echivalentul backtracking-ului pentru toate starile S.
Dupa ce obtinem sirul V putem raspunde la orice intrebare in O(1). Complexitatea totala a solutie este O( N + M + 2L * L ).
Secv9
Fie A vectorul iniţial şi Sum vectorul sumelor parţiale. Vectorul Sum se calculează după următoarea recurenţă: Sumi = Sumi-1+Ai. O subsecvenţă [i, j] a vectorului iniţal are suma mai mare sau egală ca S dacă Sumj-Sumi-1 ≥ S. Ordonăm crescător vectorul sumelor parţiale. Parcurgem apoi vectorul cu doi indici i şi j, unde i reprezintă indicele sumei curente, iar j indicele celei mai mari sume care respectă proprietatea Sumi-Sumj >= S. Această parcurgere are complexitate O(N), deoarece iteraţia cu j se continuă de la valoarea lui j pentru i-1, fiecare element al vectorului fiind astfel vizitat o singură dată. Este evident că cea mai lungă subsecvenţă cu proprietatea dorită care se termină pe poziţia i are lungimea egală cu i - min{pozitia lui Sumk | k ≤ j}. Acest minim poate fi actualizat în O(1) la fiecare incrementare a lui j. Rezultatul căutat este maximul lungimilor subsecvenţelor pentru fiecare i.
Complexitatea totală este O(NlogN) din cauza sortării.
Redu
Problema se poate rezolva cu programare dinamica. Fie din[i][j] = costul minim cu care pot sa reduc secventa dintre pozitiile i si j. Ca sa determinam din[i][j] putem sa ne gandim in urmatorul fel: primul caracter (cel de pe pozitia i) il putem reduce ultimul cu un alt caracter de pe o pozitie oarecare k din subsecventa, fara a afecta in nici un fel optimalitatea solutiei. Dar pentru aceasta trebuie mai intai sa reducem secventa (i + 1, k - 1) si secventa (k + 1, j) si apoi sa reducem cele doua caractere ramase. Vizual:
i ___S1___ k _____S2_____j
Pentru a reduce caracterul de pe pozitia i cu cel de pe pozitia k trebuie sa reducem S1, S2 (incluzand pozitia j) si apoi cele doua caractere ramase S[i], S[k].
Asadar pentru a gasi solutia optima trebuie doar sa incercam toate k-urile posibile si sa o alegem pe cea mai buna. Astfel recurenta dinamicii se contureaza in acest mod: din[i][j] = MIN ( din[i + 1][k - 1] + din[k + 1][j] + C[ S[i] ][ S[k] ]) pentru oricare k=i+1,j. Trebuie sa avem atentie la cateva cazuri particulare:
- din[i][j], unde j - i + 1 nu este par este INFINIT (nu se poate reduce o secventa de lungime impara)
- din[i][j], unde i > j este 0 (ajungem in aceste cazuri prin recurenta noastra, dar ele reprezinta siruri vide)
- din[i][j], unde i + 1 = j este C[ S[i] ][ S[j] ] (cazul cel mai mic din dinamica ce poate fi rezolvat imediat).
Rezultatul se va gasi in din[ 1 ][ N ].
Complexitatea acestei dinamici este O(N3).
Jap2
Ştim că putem afla puterea la care apare numărul prim P în N! folosind formula [N/P] + [N/P2] + [N/P3] + ..., unde [x] reprezintă partea întreagă a lui x. Pentru un query A, B putem determina puterea la care apare P în A!, B! şi A-B! şi deci putem afla puterea la care apare P în Combinări(A, B).
În cazul în care C(A, B) este divizibil cu P, răspunsul este, evident, 0. În cazul în care C(A, B) nu este divizibil, vom încerca să determinăm rapid valoarea lui N! ignorând toţi factorii lui P.
Să luăm un exemplu pentru P = 3 şi să vedem cum arată valorile din 2!, 8! şi 26!. Vom ignora toţi factorii lui 3, deci 3 devine 1, 6 devine 2, 9 devine 1, 12 devine 4 modulo 3 = 1, etc.
Pentru 2 produsul este egal cu 1*2.
Pentru 8 produsul este egal cu (1*2)*1*(1*2)*2*(1*2).
Pentru 26 produsul este egal cu: (1*2*1*1*2*2*1*2)*1*(1*2*1*1*2*2*1*2)*2*(1*2*1*1*2*2*1*2).
Putem observa că pentru numere de forma Pk-1, cu k număr natural, valoarea lui Pk-1-1 se repetă de P ori şi în plus pe poziţiile de forma l * Pk-1 din şir se află numerele de la 1 la P-1.
De aici, reiese o idee de rezolvare: Când vrem sa calculăm N! factorial încercăm să-l reducem la probleme mai mici folosindu-ne de faptul că produsurile de mai sus se repetă.
Vom precalcula toate valorile lui x!, cu x între 1 şi P-1 şi toate valorile factorialelor pentru numere de forma Pk-1 (se poate găsi uşor relaţie de recurenţă între Pk-1-1 şi Pk-1).
Pentru a calcula N!, ne vom uita la cel mai mare număr de forma Pk-1, care e mai mic strict ca N. Putem determina de câte ori se repetă produsul de lungime Pk-1 în desfăşurarea lui N! printr-o împărţire şi câti din factorii 1, 2, ..., P-1 din afara produsurilor există. Dacă N nu este la rândul lui de forma Pk+1-1, atunci ultimul dintre produsele de forma Pk-1 va fi incomplet şi va trebui să-l calculăm recursiv în acelaşi mod descris. Adâncimea maximă pe care o avea funcţia va fi egală cu O(logP N) şi pentru că vom avea nevoie de o funcţie care să ridice o valoare la orice putere în timp logaritmic complexitatea finală va fi O(logP N * log2 P) pe test.
Având calculate factorialele A!, B! şi A-B! simplificate putem calcula combinările folosind conceptul de invers modular, care ne permite să simulăm împărţirea pe numere naturale in aritmetica modulară.
În timpul concursului am aflat din sursele concurenţilor de existenţa Teoremei lui Lucas care rezolvă aceeasi problemă, spre dezamăgirea autorului. :( Soluţia oficială prezentată mai sus poate fi extinsă însă pentru calcularea Aranjamentelor sau doar a Factorialului.
Tot prin precaluclarea factorialelor pana la puterea P se puteau obtine 70-80p. Cand avem de calculat un factorial N! il vom il vom afla in timp logaritmic calculandul astfel: N = pwr( Fact [ P ] , X ) + pwr ( Fact [ R ] , Y ) + ... , unde X este prima putere a lui P mai mica decat N , unde R este N - P^X , s.a.m.d. si unde pwr reprezinta ridicarea la putere , fiecare ridicare la putere putandu-se calucula in timp logaritmic.
O abordare de 50p ar fi fost preprocesarea factorialelor pana la A.
Recurenta2
Notăm Si = 1*X1 + 2*X2 + ... + i*Xi. Recurenţa pentru Si este uşor de găsit: Si+1 = Si + (i+1)*Xi+1. Putem să-l explicităm pe Xi+1 în funcţie de termenii anteriori şi obţinem: Si+1 = Si + (i+1)*Xi-1*B + (i+1)*Xi*A + (i+1)*C. Aşadar, observăm că la pasul i nu ne dorim să cunoaştem doar valorile Xi-1, Xi şi Si, ci şi pe (i+1)*Xi-1 şi (i+1)*Xi. Recurenţele pentru aceşti 2 noi termeni sunt şi ele uşor de găsit: (i+1)*Xi-1 = i*Xi-1 + Xi-1, iar (i+1)*Xi = i*Xi + Xi = i*Xi-1*A + i*Xi-2*B + i*C + Xi-1*A + Xi-2*B + C. Observăm că putem aşeza aceste recurenţe în urmatoarea matrice de trecere de la pasul i-1 la pasul i:
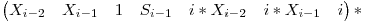

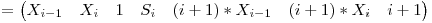 .
.
Putem aplica proprietatea de asociativitate a înmulţirii matricilor şi să înmulţim matricea de trecere cu ea însăşi de N ori şi abia după aceea să înmulţim matricea iniţială cu matricea rezultată. Complexitatea totală este O(logN), folosind exponenţierea în timp logaritmic.
Palmieri
Problema se rezolvă cu o abordare de tip greedy. Iniţial, ordonăm crescător punctele după abscisă. Primul punct trebuie să fie acoperit de un dreptunghi şi observăm că este inutil să plasăm acest dreptunghi atlfel decât cu latura verticală stângă pe acest punct. Continuăm să parcurgem punctele mai departe şi să le acoperim cu acelaşi dreptunghi până când acesta depăşeşte aria A. În acest moment, putem ignora punctele deja acoperite şi observăm că rămâne de rezolvat aceeaşi problemă pentru un număr strict mai mic de puncte. Pasul pentru determinarea numărului de dreptunghiuri necesare are complexitate O(N), deoarece vom parcurge fiecare punct în parte o singură dată. Complexitatea totală este O(NlogN) din cauza sortării iniţiale.
