Revizia anterioară Revizia următoare
Treapuri
În acest articol voi prezenta o alternativă pentru arborii binari de căutare echilibraţi, precum AVL, Red-Black Trees, Splay Trees şi B-Trees.
Ce este un Treap?
Treapul este un arbore binar în care fiecare nod conţine două informaţii:
- cheie
- prioritate
Structura de date respectă doi invarianţi:
- dacă parcurgem arborele în inordine, atunci vom obţine nodurile sortate (invariantul arborilor de căutare)
- prioritatea fiecărui nod este mai mare decât cea a fiilor săi (invariantul heapurilor)
În consecinţă, treapul este un arbore binar de căutare pentru chei şi un max-heap pentru priorităţi.
În continuare, vom presupune că toate cheile şi priorităţile din treapul T sunt distincte. În practică, presupunerea aceasta are un impact neglijabil.
Astfel, din moment ce T este un heap, nodul v cu prioritatea cea mai mare trebuie să fie rădăcina. Cum este şi un arbore binar de căutare, orice nod u cu cheie(u) < cheie(v) se găseşte în subarborele stâng al lui v, şi orice nod w cu cheie(w) > cheie(v) se găseşte în subarborele drept.
Cheile şi priorităţile determină în mod unic forma unui treap. Prin inducţie se demonstrează că treapul este arborele binar obţinut prin inserarea cheilor în ordinea descrescătoare a priorităţilor. Algoritmul de inserare este cel obişnuit pentru arborii de căutare. Astfel, cum fiecare set de priorităţi asociat nodurilor va aranja arborele într-un singur mod, probabilitatea ca arborele să fie echilibrat este rezonabil de mare, fapt datorat numărului mic al arborilor rău echilibraţi în comparaţie cu cei echilibraţi. Iată şi secretul acestei structuri de date: probabilitatea infimă de a se găsi o serie de priorităţi generate aleator care să nu menţină arborele echilibrat.
Avantaje
Structurile de date de heap şi de arbori binari de căutare sunt uşor de implementat şi de înţeles, iar treapurile sunt o combinaţie a acestor două concepte. Astfel, este suficient să fie înţeleşi cei doi invarianţi, după care implementarea se poate face cu uşurinţă în 20 de minute, fără antrenament. De obicei, la structuri ca Arbori Roşu-Negrii trebuie folosite serii de rotaţii stânga şi dreapta complexe şi analizate o multitudine de cazuri, pe când la treapuri facem doar câte o rotaţie stânga sau dreapta la fiecare pas al algoritmului. Ei nu sunt predaţi pentru că Arborii Roşu-Negrii sau AVL au demonstraţia că limita celei mai lente operaţii este O(log N) şi sunt exemple didactice, dar treapurile, deşi cu o demonstraţie mai grea pentru limita de O(log N), ce implică probabilităţi, sunt mult mai uşor de implementat iar în practică, cu siguranţă este greu de decis care sunt mai rapizi. Sunt deci, o opţiune demnă de luat în seamă. Pe lângă asta, treapurile suportă şi alte două operaţii pe care nu le putem face cu Arborii Roşu-Negrii sau cu arborii AVL. Aceste operaţii sunt join şi split.
Operaţii
Costul operaţiilor de mai jos este proporţional cu adâncimea unui nod din treap. După cum am menţionat mai sus, cu ajutorul teoriei probabilităţilor se poate deduce că adâncimea aşteptată a oricărui nod este O(log N), ceea ce implică costul celor mai lente operaţii să fie O(log N).
Căutare
Căutarea într-un treap este identică cu cea într-un arbore binar de căutare. Pentru a verifica dacă o cheie există putem proceda în felul următor:
int search(T* n, int key)
{
if (n == nil) return 0;
if (key == n->key) return 1;
if (key < n->key)
return search(n->left, key);
else
return search(n->right, key);
}Se observă că algoritmul poate fi scris şi iterativ, lucru ce este recomandat.
Rotaţii
Rotaţiile sunt cărămizile de la baza structurii de Treap.
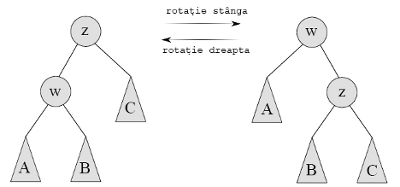
Figura 1: Rotaţiile într-un arbore binar de căutare. Nodurile sunt reprezentate de cercuri iar subarborii de triunghiuri. Ambele operaţii de rotaţie menţin invariantul arborilor de căutare.
Să urmărim efectul rotaţiilor asupra structurii de heap a unui treap care respectă doar invariantul arborilor de căutare. Aşadar, să presupunem că arborele din figura din stânga are o structură de heap cu excepţia lui w care are o prioritate mai mare decât a lui z. Dacă îl rotim pe w spre dreapta vedem în figura din dreapta că structura de heap este satisfăcută. Din moment ce A era un subarbore valid al lui w, va rămâne în continuare un subarbore valid. Cum B şi C se aflau iniţial sub z ei aveau o prioritate mai mică decât a lui z, şi, astfel, după rotaţie ei sunt subarbori valizi pentru z. Este clar că z este un fiu valid al lui w, prin presupunerea făcută iniţial.
Să urmărim dacă invariantul arborilor de căutare se menţine în urma unei astfel de rotaţii.
- În arborele din figura din stânga avem inegalităţile următoare: A < w < B, z < C, w, A, B < z. Din acestea se obţine: A < w < B < z < C.
- În arborele din figura din dreapta avem inegalităţile următoare: A < w, B < z < C, w < z, B, C. Din acestea se obţine: A < w < B < z < C.
Cum am obţinut acelaşi şir de inegalităţi, am arătat existenţa invariantului arborilor de căutare.
Reţineţi că această rotaţie împreună cu imaginea sa în oglindă, rotaţia spre stânga dacă urmărim desenul de la dreapta spre stânga, stau la baza algoritmilor de inserare şi ştergere!
Pentru o rotaţie sunt necesare doar câteva operaţii cu pointeri.
Complexitate: O(1).
Inserare
În cadrul operaţiei de inserare vom atribui unui nod nou o prioritate aleatoare şi îl vom insera, conform algoritmului standard de inserare într-un arbore binar, la baza arborelui. Cheile formează un arbore de căutare, dar priorităţile pot să nu mai formeze un heap. Pentru a redobândi această proprietate, cât timp nodul de inserat, fie el z, are prioritatea mai mare decât a părintelui său, se va executa o rotaţie în z, o operaţie locală care scade nivelul lui z cu 1 şi creşte nivelul părintelui lui z cu 1, şi care menţine invariantul arborilor de căutare. Timpul de inserare al lui z este proporţional cu adâncimea lui înainte de rotaţii - trebuie să coborâm după care să urcăm înapoi efectuând rotaţiile necesare.
Complexitate: O(log N).
Ştergere
Operaţia de ştergere este inversul operaţiei de inserare. Să presupunem că dorim să ştergem un nod z. Scopul este să îl aducem în postura de frunză pentru a-l şterge. Astfel, pentru a menţine cei doi invarianţi (exceptându-l pe z) vom alege fiul cu prioritatea mai mare şi îl vom roti în locul lui z, cât timp acesta nu este frunză. Atunci când z devine frunză îl vom şterge.
Complexitate: O(log N).
Split
Uneori dorim să despărţim treapul T în două treapuri T< şi T> astfel încât cheile din T< să conţină cheile din T mai mici decât o cheie key dată, iar T> să conţină cheile din T mai mari decât aceeaşi cheie key. Soluţia constă în inserarea unui nod ajutător z a cărui cheie este key şi prioritate infinit. După inserare, z va fi rădăcina arborelui, având prioritatea cea mai mare. Dacă ştergem rădăcina, subarborele stâng şi cel drept vor fi exact treapurile căutate.
Costul operaţiei split este egal cu costul operaţiei de inserare a lui z.
Complexitate: O(log N).
Join
Operaţia join constă în unirea a două treapuri T< şi T>, unde fiecare cheie din T< este mai mică decât oricare cheie din T>, într-un singur super-treap. Join se realizează în mod invers operaţiei de split prin crearea unei rădăcini z, ce are ca subarbore stâng pe T< iar ca subarbore drept pe T>, pe care o vom suprima. Dacă în treap avem noduri w cu key(w) = key(z) atunci acestea ar trebui să rămână.
Costul operaţiei join este egal cu costul operaţiei de ştergere a lui z.
Complexitate: O(log N).
Implementare
Mai jos este codul în C++ pentru unele operaţii prezentate anterior. Puteţi face o comparaţie între funcţiile erase sau balance din articolul următor despre arborii AVL şi cele ale treapurilor.
struct T {
int key;
int priority;
T *left, *right;
} *R, *nil;
void init(T* &R)
{
srand(unsigned(time(0)));
R = nil = new T();
nil->key = nil->priority = 0,
nil->left = nil->right = NULL;
}
void rotleft(T* &n)
{
T *t = n->left;
n->left = t->right, t->right = n;
n = t;
}
void rotright(T* &n)
{
T *t = n->right;
n->right = t->left, t->left = n;
n = t;
}
void balance(T* &n)
{
if (n->left->priority > n->priority)
rotleft(n);
else if (n->right->priority > n->priority)
rotright(n);
}
void insert(T* &n, int key)
{
if (n == nil)
{
n = new T();
n->key = key, n->priority = rand() + 1,
n->left = n->right = nil;
return;
}
if (key < n->key)
insert(n->left, key);
else if (key > n->key)
insert(n->right, key);
balance(n);
}
void erase(T* &n, int key)
{
if (n == nil) return ;
if (key < n->key)
erase(n->left, key);
else if (key > n->key)
erase(n->right, key);
else {
(n->left->priority > n->right->priority) ? rotleft(n) : rotright(n);
if (n != nil)
erase(n, key);
else {
delete n->left;
n->left = NULL;
}
}
}