| Fişierul intrare/ieşire: | xor.in, xor.out | Sursă | ONI 2010 - Baraj |
| Autor | Filip Cristian Buruiana | Adăugată de | |
| Timp execuţie pe test | 0.175 sec | Limită de memorie | 36864 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Xor
Lui Hadrianus îi plac matricele infinite care sunt generate după o anumită regulă. Înainte de primul baraj, el se gândeşte la o astfel de matrice, în care elementul de pe linia i şi coloana j este egal cu i xor j. Hadrianus doreşte să determine suma elementelor pentru unele submatrici ale matricii formate după regula de mai sus. Se numeşte submatrice de coordonate (L1, C1, L2, C2), cu 1 ≤ L1 ≤ L2 şi 1 ≤ C1 ≤ C2, o zonă dreptunghiulară din matrice care are colţul stânga-sus pe linia L1 şi coloana C1 şi colţul dreapta-jos pe linia L2 şi coloana C2.
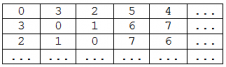
Operaţia xor reprezintă operaţia de disjuncţie exclusivă realizată pe biţii operanzilor. În Pascal, operatorul corespunzător este xor, iar în C/C++ acest operator este ^. De exemplu, 20 xor 14 = 26. Matricea formată are primele elemente conform figurii alăturate.
Scrieţi un program care citeşte coordonatele a T submatrice şi afişează pentru fiecare dintre aceste submatrice suma elementelor sale modulo P (restul împărţirii sumei la P), unde P este un număr prim.
Date de intrare
Fişierul de intrare xor.in conţine pe prima linie T şi P, cu semnificaţia de mai sus. Fiecare din următoarele T linii conţine câte 4 numere naturale L1 C1 L2 C2, despărţite printr-un spaţiu, reprezentând coordonatele unei submatrice.
Date de ieşire
Fişierul de ieşire xor.out conţine exact T linii. Linia cu numărul i conţine suma modulo P a elementelor celei de a i-a submatrice din fişierul de intrare.
Restricţii
- 1 ≤ T ≤ 20 000
- Pentru fiecare submatrice din cele T, 1 ≤ L1 ≤ L2 ≤ 108 şi 1 ≤ C1 ≤ C2 ≤ 108
- P este număr prim mai mic sau egal decât 30 000
- Liniile şi coloanele matricei sunt numerotate începând cu 1
- La evaluare se vor folosi 10 teste. Ele vor avea următoarea structură:
- Pentru primele 2 teste, T ≤ 100 şi L2, C2 ≤ 100
- Pentru testele 3 şi 4, L2, C2 ≤ 1000
- Pentru testele 5 şi 6, L1 = L2
- Pentru testele 7 şi 8, P = 2
- Celelalte două teste respectă limitele de mai sus şi nu au nicio particularitate specială
Exemplu
| xor.in | xor.out |
|---|---|
| 5 29473 1 3 2 4 2 2 12 15 10000 10000 11000 11000 123 51 54667341 1878099 1234567 1234567 1234678 1234678 | 14 1165 23799 18591 549 |
Explicaţie
Prima submatrice este formată din elementele 2, 5, 1 şi 6. Suma modulo 29473 a acestor elemente este: (2 + 5 + 1 + 6) % 29473 = 14.
