Fişierul intrare/ieşire:	tromino.in, tromino.out	Sursă	Urmasii lui Moisil 2016, Clasa a 9-a
Autor	Vlad Stoian	Adăugată de	Paul Diac •diac_paul
Timp execuţie pe test	0.25 sec	Limită de memorie	36864 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Tromino

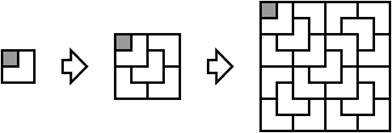
Bulbuka a primit de curând cadou un infinit de tromino-uri în formă de L. După ce s-a jucat un timp cu ele, a ajuns la următoarea concluzie: poate să acopere cu tromino-uri o tablă de dimensiuni 2^K x 2^K aproape complet (mai puţin un pătrăţel de dimensiune 1×1). Deşteapta de Bulbuka are un algoritm pentru asta: porneşte de la o configuraţie 2^K-1 x 2^K-1, o copiază de încă 3 ori, apoi roteşte 2 dintre copii şi la sfârşit, adaugă un tromino la mijloc (v-a făcut un desen mai jos, ca să înţelegeţi mai bine, pentru K = 1, 2 şi 3). Pornind de la o configuraţie de acest tip, ea a observat că poate roti la 90o câte un tromino, în sensul acelor de ceasornic sau invers, doar dacă după rotire încape înapoi pe tablă. Folosind astfel de rotaţii, pătrăţelul lipsă poate ajunge pe orice poziţie de pe tablă.
Bulbuka vă pune acum Q întrebări de tipul: care este numărul minim de rotaţii necesare pentru ca pătrăţelul lipsă să ajungă de la coordonatele (S_R, S_C) la coordonatele (F_R, F_C)?

Cerinţă

Pentru o configuraţie 2^K x 2^K , explicată în enunţ, Bulbuka vă pune Q întrebări de tipul: care este numărul minim de rotaţii de 90 grade de care avem nevoie pentru a aduce pătrăţelul lipsă din punctul (S_R, S_C) în (F_R, F_C)?

Date de intrare

Fişierul de intrare tromino.in conţine pe prima linie două valori K şi Q, unde 2^K x 2^K reprezintă dimensiunea tablei şi Q reprezintă numărul de întrebări pe care le pune Bulbuka. Fiecare din următoarele Q linii din fişier reprezintă o întrebare şi conţine valorile S_R, S_C, F_R, F_C unde (S_R, S_C) reprezintă coordonatele iniţiale ale pătrăţelului lipsă şi (F_R, F_C) reprezintă coordonatele finale la care va ajunge pătrăţelul.

Date de ieşire

Fişierul de ieşire tromino.out va conţine Q linii, ce reprezintă răspunsurile la cele Q întrebări.

Restricţii

• 1 ≤ K ≤ 60;
• 3 ≤ Q ≤ 5000;
• 0 ≤ S_R, S_C, F_R, F_C < 2^K
• Se garantează că pentru orice poziţie a pătrăţelului lipsă există o configuraţie unică a tablei
• Pentru 15% din teste K ≤ 3

Exemplu

tromino.in	tromino.out	Explicatie
2 1 1 3 0 0	4
3 5 0 0 0 1 0 0 1 1 0 0 3 3 0 0 2 4 1 0 1 0	1 2 6 8 0	.

Cum se trimit solutii?