| Fişierul intrare/ieşire: | tris.in, tris.out | Sursă | ONI 2017, clasele 11-12 |
| Autor | Eugenie Daniel Posdarascu, Lucian Bicsi | Adăugată de | |
| Timp execuţie pe test | 0.25 sec | Limită de memorie | 65536 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Tris
Ninel, fratele mai mic al lui Gigel, a primit de ziua lui un joc tetris în care toate piesele sunt formate din maxim 3 pătrăţele. Există 4 tipuri de astfel de piese care, luând în considerare rotirile pieselor, se pot plasa pe un grid în 9 moduri distincte:
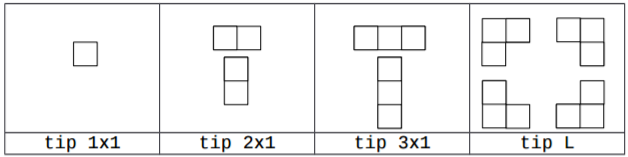
Jocul conţine din fiecare tip de piesă cel puţin 2 şi cel mult 100 de bucăţi. El doreşte să plaseze toate piesele astfel încât acestea să formeze un ciclu, adică orice pătrăţel să aibă exact doi vecini pe cele patru direcţii (sus, jos, dreapta, stânga) şi zona interioară ciclului să fie conexă pe cele patru direcţii. O mulţime de pătrăţele se consideră zonă conexă dacă din oricare pătrăţel din mulţime se poate ajunge în oricare alt pătrăţel trecând doar prin pătrăţele din mulţime pe cele patru direcţii.
Cerinţă
Cunoscând numărul de piese din fiecare tip, ajutaţi-l pe Ninel să rezolve problema.
Date de intrare
Fişierul tris.in conţine pe o singură linie 4 numere naturale a b c d, separate prin câte un spaţiu, reprezentând numărul de piese de tipul 1×1, 2×1, 3×1 respectiv L în această ordine.
Date de ieşire
Fişierul tris.out va conţine pe prima linie două numere n şi m, reprezentând dimensiunile matricei-soluţie.
Pe următoarele n linii se vor afla câte m numere naturale din mulţimea {0,1,…, a+b+c+d}, fiecare element semnificând:
- 0 – dacă pe poziţia respectivă nu se găseşte niciun element;
- i – dacă pe poziţia respectivă este plasată una din cele a+b+c+d piese, identificată cu numărul i.
Piesele pot fi numerotate în orice ordine cu numere de la 1 la a+b+c+d, cu condiţia ca acestea să aibă numere distincte.
Evaluare
O soluţie se consideră validă dacă şi numai dacă se respectă următoarele condiţii:
- dimensiunile matricei sunt cel mult egale cu 800×800;
- fiecare celulă ocupată de o piesă are exact 2 vecini;
- zona ocupată de piese formează un ciclu;
- zona interioară ciclului este conexă pe cele patru direcţii.
Restricţii şi precizări
- pentru datele de intrare problema întotdeauna are soluţie;
- pentru 30 de puncte 10 ≤ a, b, c, d ≤ 100;
- pentru 50 de puncte 5 ≤ a, b, c, d ≤ 100;
- pentru 80 de puncte 3 ≤ a, b, c, d ≤ 100;
- pentru 100 de puncte 2 ≤ a, b, c, d ≤ 100;
Exemplu
| tris.in | tris.out | Explicaţie |
|---|---|---|
| 3 4 3 4 | 11 6 0 1 2 4 4 4 1 1 0 0 0 3 8 0 0 0 3 3 8 0 0 0 9 0 8 0 0 0 9 9 10 0 0 0 0 13 10 0 0 0 0 11 12 0 0 0 0 11 12 0 0 0 0 14 6 0 0 0 0 7 6 5 5 5 7 7 | Avem 3 piese de tip 1×1 Avem 4 piese de tip 2×1 Avem 3 piese de tip 3×1 Avem 4 piese de tip L Matricea-soluţie este formată din 11 linii şi 6 coloane: 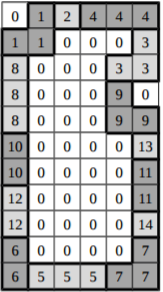
|
Observaţie:
Următorea matrice nu formează soluţie din multiple motive:
- există pătrăţele care nu au exact doi vecini (vezi piesele 6, 9, 13 şi respectiv 15);
- zona interioară ciclului nu este conexă pe cele patru direcţii. Există două zone interioare conexe cu 3 pătrăţele, respectiv 13 pătrăţele.

