| Fişierul intrare/ieşire: | tairos.in, tairos.out | Sursă | OJI 2019, clasele 11-12 |
| Autor | Radu Muntean | Adăugată de | |
| Timp execuţie pe test | 0.5 sec | Limită de memorie | 65536 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Tairos
Se dă un arbore cu N noduri, numerotate de la 1 la N.
Arborele se va transforma astfel: la oricare etapă fiecare nod de gradul 1 diferit de rădăcină din arborele
actual se înlocuieşte cu un arbore identic cu cel dat iniţial, iar la următoarea etapă procedeul se va relua
pentru arborele obţinut, formându-se astfel un arbore infinit. În următoarele 3 imagini se prezintă un
exemplu de arbore dat iniţial, arborele obţinut după prima etapă de prelungire a frunzelor şi arborele
obţinut după 2 etape de prelungire a frunzelor.
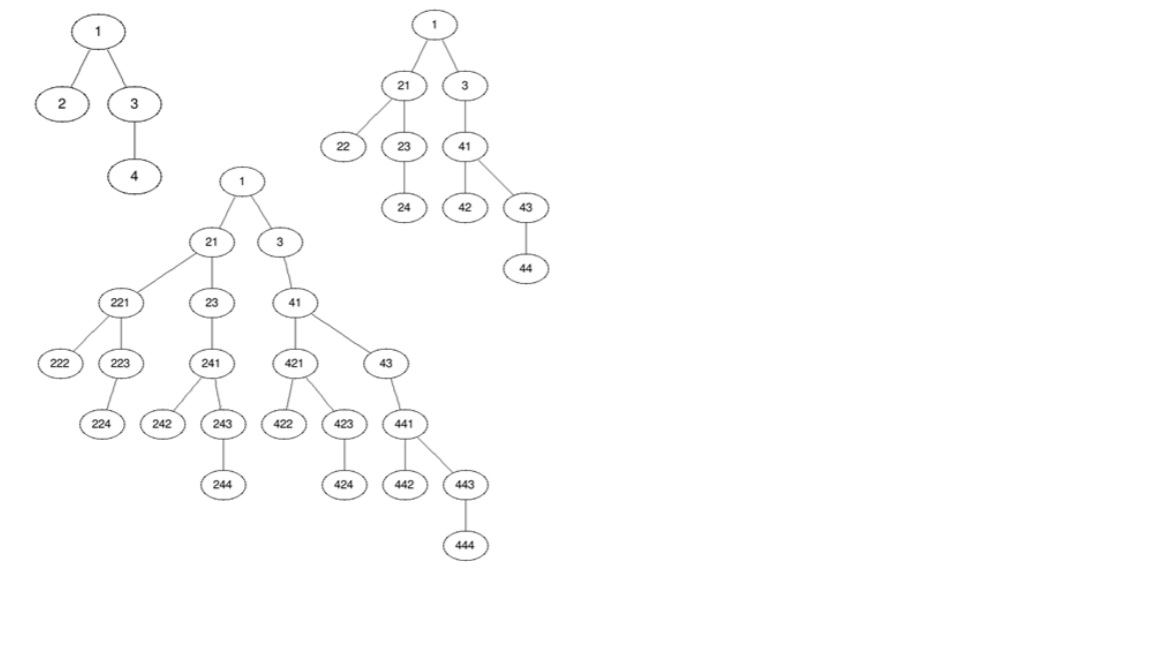
Să se determine câte noduri se află la distanţă D de rădăcina arborelui infinit.
Date de intrare
Pe prima linie a fişierului de intrare tairos.in se va afla un număr natural N, reprezentând numărul de
noduri din arborele dat iniţial. Pe a doua linie se va afla numărul întreg D, cu semnificaţia de mai sus, iar
fiecare dintre următoarele N-1 linii conţine câte 2 numere întregi x şi y cu semnificaţia că în arborele dat
iniţíal există muchia [x,y].
Date de ieşire
Fişierul de ieşire tairos.out va conţine un singur număr, şi anume restul împărţirii numărului de
noduri cerut la numărul 1.000.000.007.
Restricţii
- 2 ≤ N ≤ 100
- 1 ≤ D ≤ 10.000
- Un arbore este un graf neorientat, conex şi fără cicluri.
- Distanţa dintre două noduri x şi y ale unui arbore este egală cu numărul de muchii ale unui lanţ
cu extremităţile în nodurile x şi y, lanţ format din noduri distincte. - Rădăcina va fi considerată ca fiind nodul 1;
- Pentru teste în valoare de 17 puncte avem N = 3
- Pentru teste în valoare de alte 22 puncte răspunsul este ≤ 10 000;
Exemplu
| tairos.in | tairos.out |
|---|---|
| 4 3 1 2 3 1 3 4 | 5 |
| 5 3 1 2 3 1 3 5 4 3 | 8 |
| 5 25 2 1 2 3 1 4 5 2 | 33554432 |
Explicaţie
Pentru primul test, arborele dat în fişierul de intrare are 4 noduri. Se cere numărul
nodurilor aflate la distanţa 3 faţă de rădăcină.
Urmărind imaginile din exemplele de mai sus,la distanţa 3 avem
următoarele 5 noduri: 222, 223, 241, 421 şi 43
