| Fişierul intrare/ieşire: | semafor2.in, semafor2.out | Sursă | InfoPro, Runda 1, Grupa A |
| Autor | Andrei Constantinescu | Adăugată de | |
| Timp execuţie pe test | 0.3 sec | Limită de memorie | 256000 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Semafor2
Cum te-ai dus, asa te-ntorci!
(vechi proverb oltenesc)
Zona Gorjului este formată din N orase, legate între ele prin M drumuri unidirecţionale. Drumurile sunt de două tipuri: poteci (reprezentate prin 0) şi drumuri naţionale (reprezentate prin 1). Nea Mărin pleacă dintr-un oraş şi vrea să îşi alcătuiască un traseu cu următoarele proprietăţi:
- Traseul începe şi se termină în acelaşi oraş.
- La fiecare pas Nea Mărin se plimbă pe unul din drumurile ce au oraşul actual ca sursă, respectând sensul lui de mers. Astfel el ajunge în oraşul destinaţie al drumului, de unde procesul se reia la următorul pas.
- Pentru a nu se plictisi, peisajul trebuie să NU fie unul monoton. El consideră peisajul de pe traseu ca fiind monoton dacă traseul trece consecutiv prin două poteci sau prin două drumuri naţionale.
- De asemenea, peisajul trebuie să fie echilibrat, în sensul că numărul total de drumuri parcurse din fiecare tip trebuie să fie egal.
Voi, programatori renumiţi, sunteţi acum puşi în impas – va trebui să determinaţi din ce oraşe de început poate Nea Mărin să îşi alcătuiască un traseu cu proprietăţile descrise anterior.
Cerinţa
Date fiind cele N oraşe din Zona Gorjului, numerotate de la 1 la N, şi cele M drumuri ce leagă oraşele, fiecare fiind specificat prin cele două oraşe pe care le leagă (adică sursa şi destinaţia drumului) şi prin tipul drumului, determinaţi din care oraşe x ar putea începe Nea Marin un traseu echilibrat şi nemonoton, conform descrierii de mai sus.
Date de intrare
Pe prima linie se citesc de la tastatură numerele naturale N şi M, separate printr-un spaţiu.
Pe următoarele M linii urmează câte un triplet de numere naturale a b c, cu numere separate prin spatii şi cu semnificaţia că există un drum de la a la b ce leagă oraşele a şi b, al cărui tip este c ($0$ pentru poteci, 1 pentru drumuri naţionale).
Date de ieşire
Pe singura linie se va afişa un şir format din N cifre binare. A i-a cifra pentru 1 ≤ i ≤ N fiind 1 dacă şi numai dacă Nea Marin îşi poate alcătui un traseu echilibrat şi nemonoton care pleacă din oraşul i, de tipul celui descris în enunţ. Altfel, cifra va fi 0. Cifrele se vor afişa fără spaţii între ele!
Restricţii şi precizări
- 1 ≤ N ≤ 40.000
- 1 ≤ M ≤ 200.000
- Este posibil ca unele dintre cele M drumuri de la a la b să aibă a = b, aşa cum numai într-un sistem de drumuri oltenesc mai vezi. De asemenea, pentru unele perechi (a, b) este posibil să fie mai multe drumuri de la a la b.
- Observaţi că traseul lui Nea Mărin poate trece de mai multe ori prin acelaşi nod (vezi exemple).
- Pentru 15 puncte, N ≤ 8, M ≤ 22
- Pentru alte 17 puncte N ≤ 600, M ≤ 3.000
- Pentru alte 19 puncte se garantează că pentru oricare 51 de oraşe distincte alese dintre cele N, există printre acestea două oraşe a şi b, cu proprietatea următoare: dacă există un traseu de la a la b (indiferent de tipul de drumuri care îl compun) atunci nu exista un traseu de la b la a.
- Pentru alte 20 puncte sunt exact N drumuri naţionale, acestea fiind de la 1 la 2, de la 2 la 3, ..., de la N-1 la N şi de la N la 1.
Exemple
| semafor2.in | semafor2.out | Explicaţie | Diagrama |
|---|---|---|---|
| 3 3 1 2 0 2 3 1 3 1 1 | 000 | Exista un singur traseu 1->2->3->1. Indiferent din ce oraş ar începe Nea Marin traseul, acesta nu ar fi echilibrat, fiind format din doua drumuri naţionale şi o poteca. | 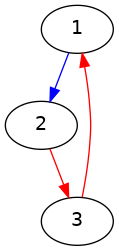
|
| 2 3 1 2 0 2 1 1 2 2 1 | 11 | Nea Marin poate parcurge traseul 1->2->1, care este atât echilibrat, cât şi nemonoton, indiferent dacă este început din oraşul 1 sau din oraşul 2. | 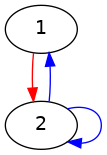
|
| 7 9 1 2 0 2 6 1 4 2 1 6 4 0 2 3 0 5 3 1 3 5 1 2 7 0 7 1 1 | 1101011 | Nea Marin poate parcurge traseul 1->2->6->4->2->7 ->1, care este atât echilibrat, cât şi nemonoton. Astfel, pentru oraşele 1, 2, 4, 6 şi 7, la poziţiile corespunzătoare se va tipări valoare 1. Pentru oraşele 3 şi 5 se observă că răspunsul este 0, deoarece nu exista poteci ce le au ca sursa. | 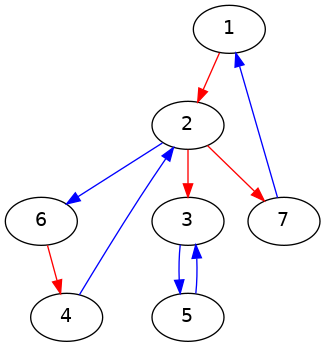
|
