Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | restrict.in, restrict.out | Sursă | Grigore Moisil 2018, 11-12 |
| Autor | Tudor Cozma | Adăugată de | |
| Timp execuţie pe test | 0.35 sec | Limită de memorie | 65536 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Restrict
Se dă un arbore cu N noduri numerotate de la 1 la N cu rădăcina în nodul 1. Fiecare muchie are asociat un cost. Pentru a ajunge din nodul 1 într-un nod D, se izolează lanţul dintre nodul 1 şi nodul D de restul arborelui, apoi se parcurg pe acest lanţ pornind din nodul 1 muchii în jos sau în sus, respectând restricţiile puse pe noduri, până când se ajunge în nodul D. Definim o restricţie pusă pe un nod X ca fiind un alt nod Y, care este strămoş al nodului X, cu semnificaţia că nu putem intra în nodul X dacă nodul Y se află printre ultimele K noduri vizitate. La fiecare trecere printr-o muchie, se adaugă la costul parcurgerii costul asociat acelei muchii.
Să se afle pentru fiecare nod i, 1 ≤ i ≤ N, în parte, care este costul minim de a ajunge din nodul 1 în nodul i, respectând restricţiile puse pe noduri, ştiind că pe drumul de la rădăcină la nodul i este prioritară minimizarea costului de a ajunge pe primul nivel, apoi pe al doilea etc. .
Date de intrare
Fişierul de intrare restrict.in conţine pe prima linie două numere întregi N şi K, cu semnificaţia din enunţ. Următoarele N-1 linii conţin câte 3 numere întregi fiecare. A i-a linie dintre aceste N-1 linii conţine următoarele 3 valori: primul număr reprezintă părintele nodului i+1, al doilea număr reprezintă costul muchiei dintre nodul i+1 şi părintele acestuia, al treilea număr reprezintă restricţia pusă pe nodul i+1, această valoare este egală cu -1 dacă pe nodul i+1 nu este pusă nicio restricţie.
Date de ieşire
Fişierul de ieşire restrict.out trebuie să conţină N linii, fiecare conţinând o singură valoare, a i-a valoare reprezentând costul minim de a ajunge din rădăcină în nodul i sau -1 în cazul în care nu se poate ajunge în acest nod.
Restricţii
- 0 ≤ N, K ≤ 100 000
- 0 ≤ costul unei muchii ≤ 1 000 000
- Pentru teste în valoare de 10 puncte, se garantează că 1 ≤ N ≤ 1 000, arborele este un lanţ (fiecare nod are cel mult un fiu) şi restricţiile nu se intersectează (dacă restricţia pusă pe nodul X este nodul Y, atunci toate nodurile dintre X şi Y sunt fără restricţii).
- Pentru alte teste în valoare de 30 puncte, se garantează că 1 ≤ N ≤ 1 000.
- Problema va fi evaluată pe teste în valoare de 90 de puncte.
- Exemplele vor reprezenta teste în valoare de 10 puncte "din oficiu".
Exemplu
| restrict.in | restrict.out |
|---|---|
| 6 3 3 2 -1 1 1 -1 1 8 -1 2 3 1 1 4 1 | 0 3 1 8 10 -1 |
| 14 6 10 20 -1 7 1 5 10 2 1 1 7 -1 9 7 11 8 0 -1 4 7 13 2 11 -1 11 3 -1 13 10 -1 3 100 -1 5 4 -1 2 165 2 | 0 44 44 32 7 106 43 43 55 24 21 144 11 -1 |
Explicaţie
Pentru primul exemplu avem arborele:
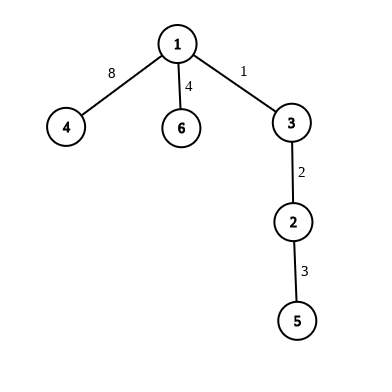
Pentru a ajunge din rădăcină în nodul 1 se observă că nu trebuie să facem nicio mutare, deci costul minim este 0.
Pentru a ajunge din rădăcină în nodul 2 cu un cost minim vom parcurge următorul traseu: 1 -> 3 -> 2, costul fiind 1 + 2 = 3.
Pentru a ajunge din rădăcină în nodul 3 cu un cost minim vom parcurge următorul traseu: 1 -> 3, costul fiind 1.
Pentru a ajunge din rădăcină în nodul 4 cu un cost minim vom parcurge următorul traseu: 1 -> 4, costul fiind 8.
Pentru a ajunge din rădăcină în nodul 5 cu un cost minim vom parcurge următorul traseu: 1 -> 3 -> 2 -> 3 -> 2 -> 5, costul fiind 1 + 2 + 2 + 2 + 3 = 10. Restricţia pusă asupra nodului 5 nu ne lasă să intrăm în acest nod dacă nodul 1 se află printre ultimele 3 noduri vizitate. De aceea, din nodul 2 mergem înapoi în nodul 3 şi apoi coborâm până în nodul 5. Astfel, ultimele 3 noduri prin care trecem înainte de a intra în nodul 5 sunt 2, 3, 2.
Nu se poate ajunge din rădăcină în nodul 6, deoarece restricţia pusă pe nodul 6 nu ne lasă să intrăm în acest nod dacă nodul 1 se află printre ultimele 3 noduri vizitate. Costul minim pentru acest nod este -1.
