| Fişierul intrare/ieşire: | rege2.in, rege2.out | Sursă | Grigore Moisil 2016, Clasele 11-12 |
| Autor | Cosmin Rusu | Adăugată de | |
| Timp execuţie pe test | 0.5 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Rege2
Regele Leonidas trebuie să-şi aleagă o armată de 300 de spartani. Surprins de mulţimea mare de voluntari care vor să-l urmeze în viitoarea luptă de la Termopile, regele are nevoie să facă o selecţie a războinicilor. Astfel, el a decis să le dea următoarea problemă:
Se dă un arbore cu N noduri (etichetate cu numere consecutive începand de la 1) cu rădăcina în nodul 1, în care fiecare muchie are asociat un cost. Se defineşte un lanţ în jos în arbore ca fiind orice lanţ simplu ce uneşte un nod A cu alt nod B din subarborele lui A. Cu alte cuvinte, un lanţ în jos este un lanţ de la A la B în care A este strămoş al lui B. Definim costul unui lanţ în jos ca fiind suma costurilor muchiilor din care este format lanţul.
Numim acoperire a unui arbore o partiţionare a muchiilor în lanţuri disjuncte, a căror reuniune este arborele iniţial. Regele Leonidas doreşte să acopere întreg arborele cu lanţuri în jos, însa are un număr limitat de lanţuri, notat în continuare cu S.
Se cere să se determine cel mai mic numar K pentru care să existe o partiţionare completă a arborelui cu maxim S lanţuri astfel încat costul fiecărui lanţ să fie cel mult K. Dacă nu există un astfel de număr K, să se afişeze -1.
Pentru că şi tu vrei să lupţi alături de Leonidas pentru libertatea Spartei, trebuie să rezolvi această problemă ca să-ţi asiguri un loc în primii 300 de spartani.
Leonidas este un rege înţelept. Ca să se asigure că nu vor exista Spartani care vor încerca să ghicească rezultatul, el vă cere să răspundeţi la T astfel de probleme.
Date de intrare
Fişierul de intrare rege.in conţine pe prima linie numarul T, reprezentând numărul de teste din fişier. Urmează apoi cele T teste. Fiecare test este descris pe mai multe linii din fişier. Pe prima linie se află numerele N si S. Pe următoarele N-1 linii se află câte trei numere x y z, cu semniţicatia că există o muchie între nodurile x si y de cost z.
Date de ieşire
Fişierul rege.out trebuie să conţină T linii: pe linia i se află răspunsul pentru testul cu numarul i.
Restricţii
- 1 ≤ T ≤ 5
- 1 ≤ N, S ≤ 100 000
- 1 ≤ Costul oricărei muchii ≤ 10 000
Exemplu
| rege2.in | rege2.out |
|---|---|
| 2 10 6 2 1 1 3 2 1 4 1 3 5 3 1 6 5 2 7 5 3 8 2 2 9 8 3 10 5 2 6 4 2 1 4 3 2 3 4 3 2 5 4 2 6 4 4 | 4 4 |
Explicaţie
Avem T = 2 teste.
Pentru primul test, avem un arbore cu N = 10 noduri. Dorim să acoperim arborele cu maxim S = 6 lanţuri. Arborele se poate acoperi cu următoarele lanţuri:
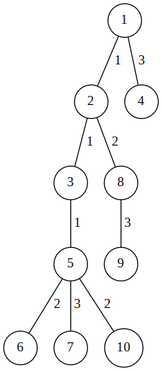
- 1-4 (cost 3)
- 1-2-8 (cost 3)
- 8-9 (cost 3)
- 2-3-5-6 (cost 4)
- 5-10 (cost 2)
- 5-7 (cost 3)
Sunt exact 6 lanţuri (maxim 6 avem voie), iar costul cel mai mare al unui lanţ e 4. Nu se poate face o acoperire cu cost maxim mai mic cu cel mult 6 lanţuri.
Pentru cel de-al doilea test, arborele are N = 6 noduri si dorim să-l acoperim cu maxim 4 lanţuri. Arborele se poate acoperi cu urmatoarele lanţuri:
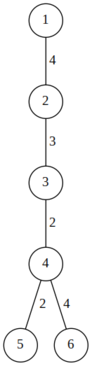
- 1-2 (cost 4)
- 2-3 (cost 3)
- 3-4-5 (cost 4)
- 4-6 (cost 4)
Sunt exact 4 lanţuri (maxim 4 avem voie), iar costul cel mai mare al unui lant e 4. Nu se poate face o acoperire cu cost maxim mai mic cu cel mult 4 lanţuri.
