Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | rayman.in, rayman.out | Sursă | Junior Challenge 2015 |
| Autor | Chichirim George | Adăugată de | |
| Timp execuţie pe test | 1.6 sec | Limită de memorie | 262144 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Rayman
Cred ca toata lumea s-a jucat Rayman si ii cunoaste protagonistul.
Au aparut planşe noi in renumitul joc si voi aveti datoria de a-i spune lui Rayman pe unde sa mearga. O plansa este alcatuita din mai multi munti de diferite inaltimi pe varful carora se afla cate un obstacol cu un grad de risc anume. Mai exact, planşa arata ca o matrice cu N linii si M coloane, iar fiecare casuta din matrice reprezinta un munte cu obstacolul sau. Deoarece Mister Dark, Admiral Rezorbeard, Andre si The Magician si-au unit fortele si au inventat o potiune care sa-i alunge lui Rayman puterea de a zbura, acesta poate sa sara de pe un munte numai pe altul cu inaltime mai mica sau egala. Stim cu totii ca lui Rayman ii place cel mai mult aventura, asa ca acesta doreste sa treaca prin cat mai multe obstacole, dar mai stim ca Rayman este un om superstitios, asa ca el nu vrea sa se intoarca din drum (aceste crede ca Mister Unlucky o sa dea navala peste el si o sa-l omoare).
Mai exact, daca la un moment dat el se afla pe un munte pe linia x si coloana y atunci in viitor el poate sa ajunga pe un munte pe linia x si coloana y1 doar daca y < y1 (cu alte cuvinte, daca insiruirea de mutari este 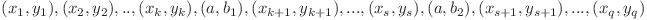 ; atunci nu este permis ca
; atunci nu este permis ca 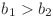 ). Totusi noi mai stim ca la cat de neinfricat este Rayman, el nu doreste sa isi asume foarte multe riscuri, asa ca voi trebuie sa ii alegeti un drum care sa treaca prin cat mai multe obsacole, dar cu gradul total de risc minim. Pentru ca lui nu ii place sa piarda timpul alegand din mai multe trasee si doreste sa plece la drum cat mai repede posibil, acesta va garanteaza ca exista o singura multime de obstacole cu cardinal maxim care poate fi parcursa in conditiile de mai sus, care sa aiba un grad total de risc minim (drumul propriu-zis nefiind neaparat unic).
). Totusi noi mai stim ca la cat de neinfricat este Rayman, el nu doreste sa isi asume foarte multe riscuri, asa ca voi trebuie sa ii alegeti un drum care sa treaca prin cat mai multe obsacole, dar cu gradul total de risc minim. Pentru ca lui nu ii place sa piarda timpul alegand din mai multe trasee si doreste sa plece la drum cat mai repede posibil, acesta va garanteaza ca exista o singura multime de obstacole cu cardinal maxim care poate fi parcursa in conditiile de mai sus, care sa aiba un grad total de risc minim (drumul propriu-zis nefiind neaparat unic).
Dar pentru ca jocul a evoluat destul de mult de la prima aparitie din 1995, si pentru ca suntem in anul 2015, si pentru ca am reusit sa scapam cu bine de anul 2013, exista un coeficient de energie, si anume: avem o matrice patratica E de dimensiune N cu semnificatia E[i][j] este energia consumata pentru a sari de pe un munte care se afla pe linia i pe un munte care se afla pe linia j. Bineinteles, Rayman vrea sa aibe cat mai multa energie pentru obstacole asa ca voi trebuie sa-i alegeti un drum care sa consume si cat mai putina energie. Rayman poate sa inceapa de oriunde.
Rayman o sa va rasplateasca cu 100 de puncte daca il ajutati sa treaca de toate planşele.
Date de intrare
Pe prima linie a fisierului rayman.in se afla douna numere natural N si M cu semnificatiile de mai sus. Pe urmatoarele N linii se afla cate M numere care reprezinta inaltimile muntilor. Fisierul de intrare mai contine inca N linii a cate M numere care reprezinta gradul de risc al obstacolelor. Pe urmatoarele N linii se afla cate N numere care reprezinta matricea E.
Date de ieşire
In fisierul rayman.out trebuie sa se afle 3 numere Nrmax, Riscmin si Energmin despartite prin cate un spatiu. Nrmax reprezinta numarul maxim de obstacole, Riscmin reprezinta riscul minim asumat pentru a parcurge Nrmax obstacole, iar Energmin este energia minima consumata pentru a parcurge Nrmax obstacole cu gradul de risc Riscmin.
Restricţii
* 1 ≤ N ≤ 15
* 1 ≤ M ≤ 100000
* 1 ≤ inaltimea unui munte ≤ 1000000
* 0 ≤ riscul asumat travesrsarii unui obstacol ≤ 10^9
* 0 ≤ energia consumata pentru o saritura ≤ 1000
* E[i][i] = 0, pentru 1 ≤ i ≤ N
***Subtask 1 (10 puncte)**:
• 1 ≤ M ≤ 1000
• inaltimile muntilor sunt numere distincte
***Subtask 2 (20 puncte)**:
• 1 ≤ N ≤ 8
• 1 ≤ M ≤ 1000
***Subtask 3 (30 puncte)**:
• E[i][j]=0, 1 ≤ i ≤ N, 1 ≤ j ≤ N
***Subtask 4 (40 puncte)**:
• Restrictiile initiale
Va rugam sa folositi urmatoarea secventa pentru a citi datele de intare:
#include <cstdio>
using namespace std;
class InputReader {
public:
InputReader() {}
InputReader(const char *file_name) {
input_file = fopen(file_name, "r");
cursor = 0;
fread(buffer, SIZE, 1, input_file);
}
inline InputReader &operator >>(int &n) {
while(buffer[cursor] < '0' || buffer[cursor] > '9') {
advance();
}
n = 0;
while('0' <= buffer[cursor] && buffer[cursor] <= '9') {
n = n * 10 + buffer[cursor] - '0';
advance();
}
return *this;
}
private:
FILE *input_file;
static const int SIZE = 1 << 17;
int cursor;
char buffer[SIZE];
inline void advance() {
++ cursor;
if(cursor >= SIZE) {
cursor = 0;
fread(buffer, SIZE, 1, input_file);
}
}
};
int main()
{
InputReader cin("rayman.in");
int n;
cin>>n;
//afisarea se face normal
}Exemplu
| rayman.in | rayman.out |
|---|---|
| 3 8 3 2 4 6 2 1 4 2 5 8 7 6 11 4 9 10 1 1 14 12 5 8 10 20 1 1 5 4 1 1 4 6 5 1 2 1 6 1 8 10 3 3 1 1 1 2 3 2 0 1 2 3 0 2 2 1 0 | 11 12 7 |
Explicaţie
Traseul pe care il urmeaza Rayman este: 3,3->3,4->2,2->2,3->2,4->3,5->2,6->1,1->1,2->1,5->1,6
