Fişierul intrare/ieşire:	parc.in, parc.out	Sursă	OJI 2012 - clasele 11-12
Autor	Zoltan Szabo	Adăugată de	Simoiu Robert •SpiderMan
Timp execuţie pe test	0.05 sec	Limită de memorie	36864 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Parc

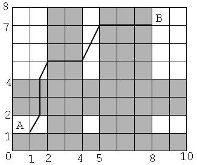
Un parc de formă dreptunghiulară este format din zone pietonale şi piste de biciclete. Reprezentând harta parcului într-un sistem cartezian, cu coordonata colţului stânga-jos (0, 0), pistele de biciclete sunt reprezentate prin dungi orizontale sau verticale colorate cu gri, iar zonele pietonale au culoarea albă, ca în figura din dreapta.
Vizitatorii parcului se pot plimba liber pe zonele pietonale în orice direcţie, însă pistele de biciclete se vor traversa, în linie dreaptă, paralel cu axele. În figura alăturată avem un parc de dimensiuni 10 × 8, cu piste de biciclete verticale între 2 şi 4 respectiv 5 şi 8, şi orizontale între 0 şi 1 respectiv între 2 şi 4. Gigel se află în punctul A(1 , 1) şi poate sa ajungă pe drumul cel mai scurt la prietenul lui, în punctul B(8 , 7) deplasându-se astfel: porneşte din punctul (1, 1) şi parcurge un traseu format din segmente cu extremităţile în punctele de coordonate (1.5 , 2) (1.5, 4) (2 , 5) (4 , 5) (5 , 7) şi în final ajunge în punctul de coordonate (8 , 7).
Lungimea totală a drumului va fi aproximativ 11.4721359.

Cerinţă

Cunoscând înălţimile celor n cote prin care va trece telecabina şi suma de care dispune Bobi, scrieţi un program care determină:

1. Lungimea totală a traseului telecabinei măsurat între cota 1 şi cota N.
2. Timpul minim exprimat în ore de care are nevoie Bobi ca să ajungă la o cotă de pe drum cu numărul de ordine mai mare sau egal cu K dat, ştiind că porneşte de la cota 1 şi că există cel puţin o variantă care conduce la acest timp minim şi care necesită o sumă mai mică sau egală cu S.

Date de intrare

Fişierul de intrare telecab.in conţine pe prima linie trei numere naturale N K S separate prin câte un spaţiu.
Pe fiecare dintre următoarele N linii se găseşte câte un număr natural. Pe linia i+1 se găseşte numărul H_i, exprimat în kilometri, reprezentând înălţimea cotei i (i = 1, 2, ..., N).

Date de ieşire

Fişierul de ieşire telecab.out va conţine pe prima linie un număr întreg L, reprezentând lungimea totală a traseului telecabinei, între cotele 1 şi N, exprimat în kilometri. Pe linia a doua se va scrie numărul natural Tmin, reprezentând timpul minim de care are nevoie Bobi ca să atingă o cotă având numărul de ordine mai mare sau egal cu K.

Restricţii

• 3 ≤ N ≤ 100 000
• 1 ≤ H₁, H₂, ..., H_N ≤ 10
• 1 ≤ K, S ≤ 1 000
• Distanţa dintre două cote succesive de pe traseu se calculează ca fiind partea întreagă a distanţei euclidiene în plan dintre cele două cote
• Între două cote consecutive, profilul muntelui este un segment de dreaptă care uneşte cotele
• Pentru toate cazurile de test se garantează că Bobi are suficienţi bani pentru a atinge sau a depăşi cota K
• Pentru mişcarea rectilinie cu viteza constantă, distanţa = viteza × timpul
• Pentru rezolvarea primei cerinţe se obţine 20% din punctajul fiecărui test

Exemplu

telecab.in	telecab.out	Explicaţie
9 8 7 4 5 2 2 1 3 5 3 3	12 9	Exemplul este cel din figură. Lungimea traseului telecabinei este: 1 + 3 + 3 + 2 + 2 + 1 = 12 Timpul minim de deplasare până la cota 8 este: 1 + 1 + 3 + 2 + 2 = 9 Segmentul [1, 2] se parcurge în 1 ore şi se cheltuie 1 euro. Segmentul [2, 3] se parcurge în 1 ore şi se cheltuie 3 euro. Segmentul [3, 6] se parcurge în 3 ore şi se cheltuie 1 euro. (distanţa de la cota 3 la cota 6 este: 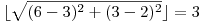, iar timpul este 3 / 1 = 3). Segmentul [6, 7] se parcurge în 2 ore şi se cheltuie 2 euro. Segmentul [7, 8] se parcurge în 2 ore şi se cheltuie 0 euro.
5 3 2 1 2 2 3 1	5 3	Lungimea traseului telecabinei este:  1 + 2 + 2 = 5 Timpul minim de deplasare până la cota 4 este: 1 + 2 = 3 Segmentul [1, 2] se parcurge în 1 ore şi se cheltuie 1 euro. Segmentul [2, 4] se parcurge în 2 ore şi se cheltuie 1 euro. Se observă că telecabina atinge cotele 2 şi 4, trecând pe deasupra cotei 3.

Cum se trimit solutii?