| Fişierul intrare/ieşire: | origami2.in, origami2.out | Sursă | ONI 2017, Baraj |
| Autor | Eugenie Daniel Posdarascu, Lucian Bicsi | Adăugată de | |
| Timp execuţie pe test | 1 sec | Limită de memorie | 131072 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Origami2
Tocmai ai primit o foaie dreptunghiulară (foarte mare) de dimensiuni N ⨯ M, împărţită în pătrăţele de 1 ⨯ 1. Fiecare pătrăţel este colorat pe ambele părţi cu una din cele 26 de culori existente în univers, identificată pentru simplitate printr-un caracter mic al alfabetului englez. Neavând ceva mai bun de făcut în timpul probei de baraj, te-ai gândit să înveţi origami. Totuşi, cum nu oricine este maestru în origami şi acest sport necesită experienţă şi viziune
artistică (lucruri pe care, bineînţeles, le vei dobândi cu timpul), ai hotărât că, pentru început, este mai interesant să împătureşti foaia într-un mod clar stabilit.
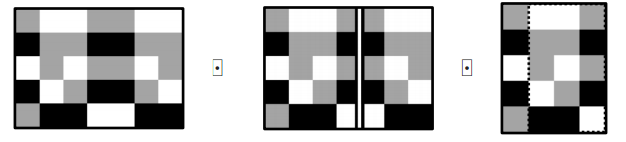
Mai exact, la fiecare pas vei alege o dreaptă (orizontală sau verticală) situată între două linii (respectiv coloane) consecutive şi vei “îndoi” jumătatea mai mică peste cea mare doar dacă culorile se vor suprapune perfect.
Un exemplu de o astfel de îndoire validă este prezentat în dreapta paginii.
După orice îndoire vei obţine un nou model (bineînţeles, de dimensiuni mai mici). În cazul în care cele două jumătăţi sunt egale, ambele variante de îndoire sunt valide. Maestru în algoritmi şi structuri de date eficiente, observi imediat că, după orice îndoitură, modelul rezultat va constitui o submatrice din modelul iniţial.
Natural, îţi vine următoarea întrebare:
“Câte submatrice distincte pot obţine, îndoind foaia de un număr arbitrar de ori (sau deloc), fără a roti foaia sau a o întoarce pe cealaltă parte?”
Formal, două submatrice se consideră distincte, dacă măcar unul din cele patru colţuri diferă de la o submatrice la alta (ca indici).
Date de intrare
Fişierul origami2.in conţine pe prima linie numerele naturale N şi M separate printr-un spaţiu, iar pe următoarele N linii se află câte un şir de caractere de lungime M, reprezentând configuraţia culorilor foii iniţiale.
Date de ieşire
Fişierul origami2.out va conţine un singur număr natural pozitiv X, reprezentând numărul de submatrice distincte care se pot obţine aplicând operaţiile din enunţ.
Restricţii
- Pentru toate testele: 1 ≤ N ≤ M, N * M ≤ 1.000.000
- Pentru 10 puncte: M ≤ 10
- Pentru 30 de puncte: M ≤ 40
- Pentru 50 de puncte: M ≤ 600, X ≤ 100.000
- Pentru 70 de puncte: M ≤ 1.000
- Din motive de performanţă, se recomandă citirea întreagă a liniilor, nu caracter cu caracter.
Exemplu
| origami2.in | origami2.out | Explicaţie |
|---|---|---|
| 5 7 baabbaa cbbccbb ababbab cabccba bccaacc | 2 | Este exemplul din desenul de mai sus. Singurele răspunsuri posibile sunt matricea iniţială, respectiv submatricea de după aplicarea operaţiei evidenţiate în figură. |
| 3 3 zzz zzz zzz | 36 | Pentru acest exemplu, orice submatrice este validă. |
