| Fişierul intrare/ieşire: | misiune.in, misiune.out | Sursă | ad-hoc |
| Autor | Adăugată de | ||
| Timp execuţie pe test | 0.15 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Misiune
Eşti un super-erou în anul 2222 şi ai primit următoarea misiune: pornind de pe planeta ta natală, Ilop, va trebui să încerci să ajungi pe Acinhet, altfel lumea va fi distrusă de o armată de monştri verzi.
Pentru a putea îndeplini acest lucru, îţi este dată harta universului: N planete şi M conexiuni interplanetare bidirecţionale ce leagă aceste planete între ele, fiecare necesitând un timp de parcurgere şi o anumită cantitate de combustibil pentru a fi parcursă.
Deoarece te deplasezi cu viteza luminii, regulile cu care eşti obişnuit nu mai funcţionează, iar timpul total se va obţine prin înmulţirea timpilor de pe parcurs.
Există unele planete cheie pe care îţi poţi alimenta nava. O planetă cheie are proprietatea că o dată cu dispariţia ei (din cauza unei catastrofe de proporţii, să zicem), s-ar pierde legatură între cel puţin două planete între care acum există drum (*un drum* este format din una sau mai multe conexiuni interplanetare).
La plecare eşti pus să îţi alegi o navă, din cele K disponibile, pentru fiecare dintre ele fiind specificată capacitatea rezervorului. Urmăreşti să poţi parcurge drumul de la Ilop la Acinhet în timp minim, dar, de asemenea, fiind vremuri de criză, şi să alegi nava cu capacitatea rezervorului minimă care îţi permite acest lucru. Nu uita că îţi poţi reumple rezervorul pe parcurs, dacă ajungi pe o planetă cheie.
Cerinţă
Va trebui să analizezi harta prezentată şi să determini timpul minim în care poţi ajunge şi nava aleasa (cea cu capacitatea minimă pentru care se obţine acest timp), precum şi drumul pe care îl vei alege. Deoarece timpul minim poate fi un număr foarte mare, nu trebuie să afli decît ultimele 6 cifre ale sale, ca să poţi verifica la destinaţie corectitudinea calculelor tale.
Date de intrare
Datele de intrare se vor citi din fişierul misiune.in:
- pe prima linie N, M şi K, separate de câte un spaţiu, cu semnificaţia din enunţ
- pe a 2-a linie numerele prin care sunt codificate planeta de start şi planeta destinaţie
- pe a 3-a linie K numere întregi capi reprezentând capacităţile navelor dintre care poţi alege
- în continuare, m linii de forma: xi yi ti ci, cu semnficaţia: de la xi la yi (şi de la yi la xi) se poate ajunge în ti unităţi de timp folosind o cantitate ci de combustibil
Date de ieşire
Datele de ieşire se vor scrie în fişierul misiune.out:
- pe prima linie TMin6 şi CapMin, reprezentând ultimele 6 cifre ale timpul minim de parcurgere şi capacitatea minimă a navei cu care se poate obţine acest timp
- pe a 2-a linie numerele planetelor ce se află pe drumul parcurs de la start la destinaţie
Restricţii şi precizări
- 2 ≤ N ≤ 1 000
- 1 ≤ M ≤ 30 000
- 1 ≤ K ≤ 10 000
- 2 ≤ ti ≤ 1 000, 1 ≤ ci ≤ 1 000, 1 ≤ i ≤ M
- capi ≤ 1 000, 1 ≤ i ≤ K
- Fie T timpul minim de parcurgere a drumului. Capacitatea rezervorului este minimă dacă pentru o navă de capacitate mai mică am obţine un timp de parcurgere mai mare decât T.
- Se garantează că pentru toate testele se va putea alege o navă cu care să poată fi parcurs drumul.
- Dacă există mai mult decât un drum ce respectă condiţiile cerute, se poate afişa oricare dintre acestea.
- Atenţie! Doar pentru 70% din teste, timpul minim de parcurgere se va încadra într-un unsigned long long int.
Exemplu
| misiune.in | misiune.out |
|---|---|
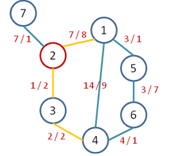
| 7 8 6 1 4 6 5 9 8 7 10 1 2 7 8 1 4 14 9 1 5 3 1 2 3 1 2 2 7 7 1 3 4 2 2 4 6 4 1 5 6 3 7 | 000014 8 1 2 3 4 |
Explicaţie
2 este planeta cheie (prin dispariţia ei nu s-ar mai putea ajunge în 7). Alegem nava de capacitate 8 şi putem parcurge 1 – 2. În 2 alimentăm cu combustibil şi parcurgem şi restul drumului: 2 – 3 – 4. Rezultă un timp total de 7 * 1 * 2 = 14.
Alegând drumul 1 – 4, am fi obţinut acelaşi timp, dar am fi avut nevoie de o navă de capacitate mai mare.