Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | logic3.in, logic3.out | Sursă | OJSEPI 2021, clasa a 9-a |
| Autor | Alin Burta | Adăugată de | |
| Timp execuţie pe test | 0.05 sec | Limită de memorie | 32768 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Logic3
Costel este pasionat de circuitele logice. El are la dispoziţie două tipuri de circuite logice simple: circuit ŞI, respectiv circuit SAU.
Circuitele logice simple au două intrări şi o ieşire.
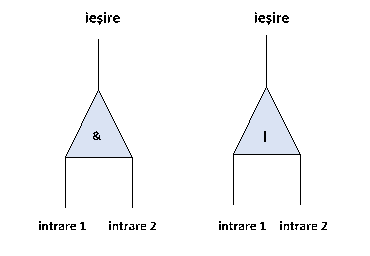
La fiecare intrare în circuit se poate introduce un bit 0 sau un bit 1 , iar circuitul este capabil să calculeze operaţia logică respectivă (ŞI ori SAU) şi să trimită rezultatul obţinut la ieşire.
Costel a învăţat că poate combina mai multe circuite simple pentru a obţine circuite complexe astfel: leagă ieşirea unui circuit de orice tip la una din intrările altui circuit, deci rezultatul obţinut la ieşirea dintr-un circuit se transmite la intrarea celuilalt. In acest fel se pot construi circuite complexe, care au mai multe intrări şi o singură ieşire.
Ultima descoperire a lui Costel este circuitul logic piramidal (prescurtat CLP), care are structura următoare:
- Circuitul cu un singur nivel este cel mai simplu tip de circuit şi este compus dintr-un circuit ŞI ori dintr-un circuit SAU;
- Pentru un circuit cu mai multe nivele avem:
- pe nivelul 1 se găseşte un singur circuit (ŞI ori SAU);
- pe nivelul 2 se găsesc două circuite simple de oricare tip; ieşirea primului circuit este conectată la intrarea 1 a circuitului de pe nivelul 1, iar ieşirea celui de-al doilea circuit este conectată la intrarea 2 a circuitului de pe nivelul 1;
- pe nivelul N sunt 2N-1 circuite simple; ieşirile primelor două circuite de pe linia N sunt conectate la intrările primului circuit de pe nivelul N-1, ieşirile următoarelor două sunt conectate la intrările celui de-al doilea circuit de pe linia N-1 etc;
Exemplu de CLP cu 2 nivele:
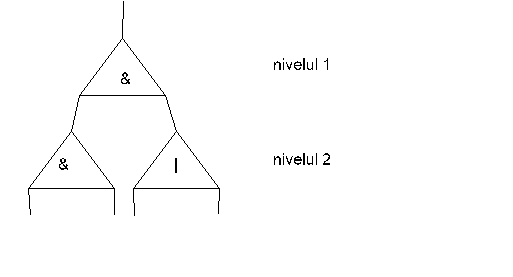
Intr-un CLP cu N nivele avem 2N intrări, corespunzătoare circuitelor de pe nivelul N. La fiecare intrare se poate introduce
un bit 0 sau un bit 1, deci un şir de 2N biţi.
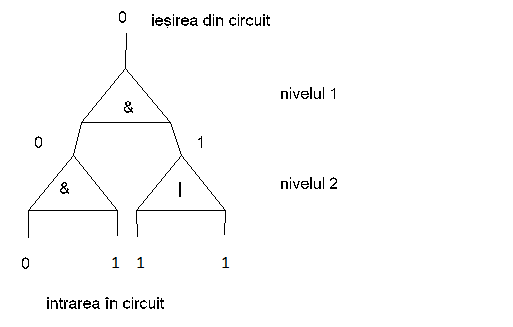
Pentru circuitul din figura de mai sus presupunem că la cele patru intrări ale circuitelor de pe nivelul 2 avem, în ordine, biţii 0111 . La ieşirea din circuit (ieşirea circuitului simplu de pe primul nivel) se obţine valoarea 0, deoarece acest circuit este echivalent cu expresia logică ((0 şi 1) şi (1 sau 1)).
Cerinţa 1 (30 de puncte)
Pentru un CLP dat, cu N nivele şi pentru K şiruri de biţi date la intrarea circuitului, să se determine, pentru fiecare şir, valoarea calculată la ieşirea din circuit.
Cerinţa 2 (70 de puncte)
Pentru un CLP dat, cu N nivele şi cunoscând valoarea obţinută la ieşire ( 0 sau 1 ), să se determine numărul şirurilor de biţi distincte ce pot fi date la intrare pentru a se obţine valoarea specificată la ieşire. Rezultatul poate fi un număr foarte mare, de aceea el se va afişa modulo 666013.
Date de intrare
Pe prima linie a fişierului logic.in se găseşte un număr natural C ( C = 1 pentru cerinţa 1, respectiv C = 2 pentru cerinţa 2)
Pe a doua linie se găseşte numărul natural N, reprezentând numărul de nivele ale circuitului;
Pe următoarele N linii (linii de la 3 la N+2) se găseşte descrierea circuitului, fără spaţii între caractere, astfel:
- pe linia 3 un caracter '&' sau '|', unde prin caracterul '&' se codifică un circuit ŞI, iar prin caracterul '|' se codifică un circuit SAU ;
- pe linia 4 două caractere din mulţimea {'&', '|'};
- pe linia 5 patru caractere din mulţimea {'&', '|'}
- ...
- pe linia N+2 avem 2N-1 caractere din mulţimea {'&','|'}
Pentru cerinţa 1:
Pe linia N + 3 avem un număr natural K, reprezentând numărul şirurilor de biţi date la intrarea în circuit;
Pe fiecare dintre următoarele K linii avem câte un şir compus din 2N biţi (caractere 0 sau 1 ), reprezentând şirul de biţi dat la intrare;
Pentru cerinţa 2:
Pe linia N + 3 avem un număr natural din mulţimea {0, 1}, reprezentând valoarea pe care circuitul trebuie să o scoată la ieşire.
Date de ieşire
Pentru cerinţa 1 se vor afişa, în fişierul logic.out, pe linii separate, K numere naturale din mulţimea {0, 1}, cu semnificaţia din enunţ;
Pentru cerinţa 2 se va afişa, în fişierul logic.out, un număr natural cu semnificaţia din enunţ.
Restricţii
- 1 ≤ N ≤ 8
- 1 ≤ K ≤ 10
Tabelele operaţiilor logice sunt:
| x | y | x SAU y | x ŞI y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Exemplu
| logic3.in | logic3.out |
|---|---|
| 1 2 & &| 3 1101 0100 1000 | 1 0 0 |
Explicaţie
C=2 , deci rezovăm cerinţa 2.
Sunt 3 şiruri de 4 biţi pentru care se obţine valoarea 1 la ieşirea din circuit: 1101, 1110, 1111.
