| Fişierul intrare/ieşire: | hypernet.in, hypernet.out | Sursă | Summer Challenge 2007, runda 2 |
| Autor | Mugurel Ionut Andreica | Adăugată de | |
| Timp execuţie pe test | 0.075 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Hypernet
In galaxia noastra exista N planete, numerotate de la 1 la N. Fiecare planeta are un anumit numar de locuitori (planeta i are Qi locuitori). Guvernul galaxiei doreste sa construiasca o retea compusa din K hipercanale (canale de transport prin hiperspatiu) bidirectionale, fiecare hipercanal conectand 2 planete distincte. Folosind reteaua construita, fiecare locuitor al fiecarei planete va dori sa viziteze fiecare din celelalte planete. Costul transportului printr-un hipercanal este de 1 unitate monetare pentru orice locuitor al oricarei planete. Prin urmare, costul vizitarii planetei j de catre un locuitor al planetei i este egal cu numarul minim de hipercanale ce trebuie traversate pentru a ajunge de la planeta i la planeta j (vom numi acest numar disti,j). Costul total al retelei de hipercanale este egal cu suma costurilor platite de fiecare locuitor al fiecarei planete:
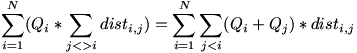
Cerinta
Determinati costul total minim al unei retele constand din K hipercanale.
Date de intrare
Prima linie a fisierului de intrare hypernet.in contine 2 numere intregi, separate printr-un spatiu: N si K. A i-a din urmatoarele N linii contine numarul intreg Qi, reprezentand numarul de locuitori ai planetei i.
Date de iesire
In fisierul de iesire hypernet.out afisati costul total minim al unei retele de hipercanale avand proprietatile specificate.
Restrictii
- 1 ≤ N ≤ 50.000
- N-1 ≤ K ≤ N*(N-1)/2
- 1 ≤ Qi ≤ 1.000.000
Exemplu
| hypernet.in | hypernet.out |
|---|---|
| 4 3 4 3 1 2 | 42 |
| 4 5 10 9 8 7 | 117 |
