Fişierul intrare/ieşire:	hiking.in, hiking.out	Sursă	AGM 2019, runda nationala
Autor	Vlad-Andrei Munteanu	Adăugată de	Patrick Sava •xtreme77
Timp execuţie pe test	1 sec	Limită de memorie	256000 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Hiking

În ţinuturile îndepărtate, a fost un munte înalt, cu multe sate care il inconjurau. Cele N sate sunt conectate prin M drumuri bidirecţionale cu lungimi intregi pozitive de cel mult 10⁹. Interesant, sătenii nu au construit mai mult de un drum între oricare doua perechi de sate şi nu au construit niciodată un drum care să înceapă şi să se termine în acelaşi sat.
Legendarul excursionist, Artskjid, a început să exploreze aceste sate. Desigur, lui i-a fost uşor să găsească lungimile celor mai scurte căi între orice pereche de sate. Cu toate acestea, acum vrea să urmărească o nouă provocare. Pentru Q perechi de sate (x, y), şi un număr întreg p din {0, 1}, el doreşte să ştie dacă există un lant (nu neaaparat simplu - adică poate vizita noduri sau muchii de mai multe ori) de la x la y de lungime l astfel încât .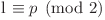

Date de intrare

Fişierul de intrare hiking.in prima linie va conţine trei numere întregi pozitive N, M, Q care reprezintă numărul de sate, numărul de drumuri şi numărul de interogări(query-uri).
Următoarele M linii vor conţine trei numere întregi pozitive a, b, c care reprezintă că există un drum bidirecţional de lungime c între oraşele a şi b.
Ultimile linii Q vor conţine trei numere întregi x, y, p care reprezintă o interogare (un query) privind satele (x, y) şi paritatea lungimii drumului p.

Date de ieşire

Fişierul de ieşire hiking.out trebuie să conţină Q linii, care descriu răspunsurile pentru query-urile date (in ordine). Răspunsul este 1 dacă Artskjid poate găsi un drum cu o lungime a parităţii date între nodurile date şi 0 altfel.

Restricţii

• 1 ≤ N ≤ 100.000
• 1 ≤ M ≤ 200.000
• 1 ≤ Q ≤ 100.000

Exemplu

Cum se trimit solutii?