| Fişierul intrare/ieşire: | harta5.in, harta5.out | Sursă | ONI 2014 Clasa a 9-a |
| Autor | Constantin Galatan | Adăugată de | |
| Timp execuţie pe test | 0.35 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Harta5
Pe baza unei imagini preluate din satelit, se realizează harta unei mici localităţi. Localitatea ocupă o suprafaţă dreptunghiulară, cu laturile orientate pe direcţiile Nord-Sud, respectiv Est-Vest. Studiind imaginea obţinută de la satelit, cartografii au constatat că toate cele k clădiri au forma unor dreptunghiuri distincte. Imaginea poate fi reprezentată sub forma unui tablou cu n x m celule aşezate pe n linii numerotate de la 1 la n şi m coloane numerotate de la 1 la m.
Numim drum, un dreptunghi al tabloului care străbate întreaga localitate pe direcţia Est-Vest şi are un număr maxim de linii sau un dreptunghi care străbate întreaga localitate pe direcţia Nord-Sud şi are un număr maxim de coloane. Drumurile, evident, nu trebuie să treacă prin clădiri.
Cartografii sunt interesaţi ca pe această hartă să fie reprezentate la scară doar clădirile, nu şi drumurile. De aceea, pentru realizarea hărţii, lăţimile drumurilor au fost reduse la o singură celulă.
Tabloul care reprezintă imaginea localităţii se codifică astfel: 1 pentru o celulă ocupată de o clădire şi 0 pentru o celulă neocupată.
Cerinta
Cunoscând n, m şi k, precum şi tabloul care codifică imaginea, se cere să se determine:
1. Numărul S de celule ocupate de către clădirea pătratică cu latura maximă şi numărul de clădiri C alese dintre celelalte k – 1 clădiri, cu proprietatea că fiecare dintre ele “încape” în interiorul clădirii pătratice cu latură maximă, fără să se suprapună peste celulele marginale ale acesteia.
2. Tabloul care reprezintă harta, în urma prelucrării imaginii iniţiale.
Date de intrare
Fişierul de intrare harta2.in conţine pe prima linie un număr natural p. Pentru toate testele de intrare, numărul p poate avea doar valoarea 1 sau valoarea 2.
Pe linia a doua se găsesc numerele naturale n, m şi k separate prin câte un spaţiu.
Pe fiecare dintre următoarele k linii, se găsesc câte patru numere naturale i1 j1 i2 j2 separate prin câte un spaţiu, primele două numere reprezentând coordonatele celulei din extremitatea Nord-Vest, iar ultimele două, coordonatele celulei din extremitatea Sud-Est pentru fiecare dintre cele k clădiri.
Date de ieşire
• Dacă valoarea lui p este 1, atunci se va rezolva numai cerinţa 1. În acest caz, în fişierul de ieşire harta2.out se vor scrie cele două numere S şi C având semnificaţia descrisă la cerinţa 1, separate printr-un singur spaţiu.
• Dacă valoarea lui p este 2, atunci se va rezolva numai cerinţa 2. În acest caz, fişierul de ieşire harta2.out va conţine tabloul care reprezintă harta obţinută pe baza imaginii din satelit. Fişierul va avea n1 linii. Pe fiecare linie se vor găsi câte m1 valori 0 sau 1 separate prin câte un singur spaţiu. Celulele situate pe marginile clădirilor vor avea valoarea 1. Celulele din interiorul clădirilor, ca şi cele din exterior, vor avea valoarea 0.
Restricţii
- 3 ≤ n, m ≤ 1500
- 1 ≤ i1 ≤ i2 ≤ n
- 1 ≤ j1 ≤ j2 ≤ m
- 1 ≤ k ≤ 1000
- 1 ≤ Lmax ≤ 50 (Lmax - latura maximă a unui dreptunghi)
- Se garantează că există soluţie pentru ambele cerinţe, pentru toate datele de test.
Exemplu
| harta5.in | harta5.out | Explicatie |
|---|---|---|
| 1 7 7 4 1 1 4 4 6 2 6 4 3 6 3 6 6 6 7 7 | 16 2 | 
|
| harta5.in | harta5.out | Explicatie |
|---|---|---|
| 2 10 11 4 1 2 4 4 8 9 8 9 7 3 9 5 2 9 3 9 | 0 1 1 1 0 0 0 0 0 1 0 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 1 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 | 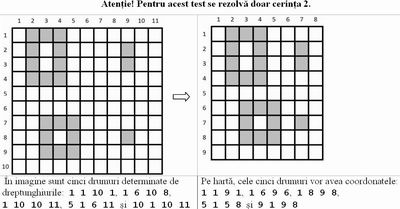
|
