| Fişierul intrare/ieşire: | fractii2.in, fractii2.out | Sursă | OJI 2014, clasele 11-12 |
| Autor | Adrian Panaete | Adăugată de | |
| Timp execuţie pe test | 0.05 sec | Limită de memorie | 65536 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Fractii2
Numărul 1 poate fi scris în diverse moduri ca sumă de fracţii cu numărătorul 1 şi numitorul o putere a lui 2. De exemplu:
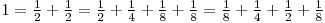
Două scrieri nu sunt considerate distincte dacă folosesc aceleaşi fracţii scrise în altă ordine. În exemplul de mai sus ultimele două scrieri nu sunt distincte.
Cerinţă
Pentru N – număr natural nenul să se determine:
a.O modalitate de scriere a numărului 1 ca sumă de exact N fracţii cu numărătorul 1 şi numitorul o putere a lui 2.
b.Numărul de scrieri distincte a numărului 1 ca sumă de exact N fracţii cu numărătorul 1 şi numitorul o putere a lui 2. Deoarece acest număr poate fi foarte mare acest număr trebuie calculat modulo 100003.
Date de intrare
Fişierul de intrare fractii2.in conţine pe prima linie un număr natural p. Pentru toate testele de intrare, numărul p poate avea doar valoarea 1 sau valoarea 2.
Pe a doua linie se găseşte un singur număr N natural – reprezentând numărul de fracţii.
Date de ieşire
Dacă valoarea lui p este 1, se va rezolva numai punctul a) din cerinţă. În acest caz, în fişierul de ieşire fractii2.out se vor scrie, pe o singură linie, N numere naturale separate prin câte un spaţiu reprezentând cei N exponenţi ai lui 2 din scrierea solicitată în prima cerinţă. Astfel, dacă numerele afişate sunt 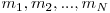 atunci există scrierea
atunci există scrierea 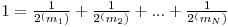
Dacă valoarea lui p este 2, se va rezolva numai punctul b) din cerinţă. În acest caz, în fişierul de ieşire fractii2.out se va scrie un număr natural reprezentând răspunsul la a doua cerinţă, adică numărul de scrieri distincte a numărului 1 ca sumă de N fracţii cu numărătorul 1 şi numitorul o putere a lui 2 (modulo 100003).
Restricţii
- 2 ≤ N ≤ 2000
- Pentru prima cerinţă se acordă 20% din punctaj.
- Pentru a doua cerinţă de acordă 80% din punctaj.
- Rezultatul pentru a doua cerinţă trebuie afişat modulo 100003
Exemplu
| fractii2.in | fractii2.out |
|---|---|
| 1 4 | 2 2 2 2 |
| 2 4 | 2 |
Explicaţie
Primul exemplu:
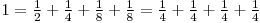
Răspunsul corespunde celei de-a doua scrieri dar există şi alte variante corecte de răspuns. De exemplu, 3 1 2 3 se consideră răspuns corect.
Atenţie! Pentru acest test se va afişa doar rezultatul la cerinţa a).
Al doilea exemplu:
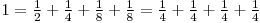
Acestea sunt singurele scrieri distincte.
Atenţie! Pentru acest test se va afişa doar rezultatul la cerinţa b).
