Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2018-03-20 17:42:32.
Revizia anterioară   Revizia următoare  

 

Fişierul intrare/ieşire:dedicatie.in, dedicatie.outSursăConcursul National de Informatica "Adolescent Grigore Moisil" 18
AutorChichirim GeorgeAdăugată deAGMinformaticaAGMInformatica •AGMinformatica
Timp execuţie pe test0.6 secLimită de memorie262144 kbytes
Scorul tăuN/ADificultateN/A

Vezi solutiile trimise | Statistici

Dedicatie

Cu totii stim ca dedcatiile la o petrecere sunt foarte scumpe. Marele artist Sorin Pastrama v-a propus un targ: daca il ajutati la rezolvarea urmatoarei probleme el va va face cate decicatii doriti la urmatoarea petrecere, PE GRATIS. Problema suna cam asa:

Se da un arbore cu N noduri. Se garanteaza ca oricum ai alege un nod pe care sa il elimini din arbore, atunci exista cel putin un subarbore din cei rezultati care are marimea 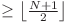\geq \left\lfloor\frac{N+1}{2}\right\rfloor .
Fie vali egal cu valoarea muchiei i. Initial vali = 0 ( 1 ≤ i ≤ N-1 ). Vom lua fiecare pereche de noduri 1 ≤ x < y ≤ N si vom incrementa cu 1 valoarea fiecarei muchii de pe drumul de la x la y. Vom sorta muchiile descrescator dupa valoarea acestora (iar in caz de egalitate, crescator dupa indicele muchiei) si le vom normaliza. Adica prima muchie din sortare va avea valoarea egala cu 0, a doua muchie va avea valoarea egala cu 1, ..., ultima muchie din sortare va avea valoarea egala cu N-2. Acum valoarea muchiei i va avea valoarea finala egala cu ( vali * alfa[vali] ) % 100003, unde alfa este un vector de lungime N-1 dat in input.

Date de intrare

Fişierul de intrare dedicatie.in ...
n
x1 y1
x2 y2
...
xn-1 yn-1
alfa0 alfa1 ... alfan-2

Date de ieşire

În fişierul de ieşire dedicatie.out ...

Restricţii

  • ... ≤ ... ≤ ...
    n <= 10^5
    1 <= alfa < 100003

Exemplu

dedicatie.indedicatie.out
6
5 4
4 2
3 1
4 6
1 5
7574 2 1 66670 25002
4
5
2
1
6
3

Explicaţie

...

Trebuie sa te autentifici pentru a trimite solutii. Click aici

Cum se trimit solutii?