Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | cuplaj.in, cuplaj.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de |  Lucian Bicsi •retrograd |
| Timp execuţie pe test | 0.1 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Poti vedea testele pentru aceasta problema accesand atasamentele.Vezi solutiile trimise | Statistici
Cuplaj maxim in graf bipartit
Se dă un graf neorientat bipartit G = (V = (L, R), E). Un cuplaj în G este o submulțime de muchii M astfel încât pentru toate vârfurile v din V, există cel mult o muchie în M incidentă în v. Un cuplaj maxim este un cuplaj de cardinalitate maximă.
Cerința
Dându-se un graf neorientat bipartit G să se determine un cuplaj maxim.
Date de intrare
Fișierul de intrare cuplaj.in conține pe prima linie trei numere naturale N, M și E, unde N reprezintă cardinalul mulțimii L iar M cardinalul mulțimii R. Pe următoarele E linii se vor afla câte două numere naturale, separate între ele printr-un spațiu, u și v, cu semnificația că există muchie de la nodul u din L la nodul v din R.
Date de ieșire
În fișierul de ieșire cuplaj.out veți afișa pe prima linie un singur număr reprezentând cuplajul maxim. Pe fiecare din următoarele linii veți afișa câte două numere x și y, separate între ele prin spațiu, cu semnificația că nodul x din L a fost cuplat cu nodul y din R.
Restricții
- 1 ≤ N, M ≤ 10 000
- 0 ≤ E ≤ minim(100 000, N * M)
- Pentru 20% dintre teste: 1 ≤ N ≤ 100, 1 ≤ M ≤ 20
- Pentru 50% dintre teste: 1 ≤ (N + M) * E ≤ 5*106
- Pentru determinarea corectă a cuplajului maxim se va acorda 40% din punctaj și încă 60% dacă s-a determinat o submulțime M validă.
Exemplu
| cuplaj.in | cuplaj.out |
|---|---|
| 5 4 9 1 1 1 2 2 1 2 2 2 3 3 2 4 2 5 2 5 4 | 4 1 1 2 3 3 2 5 4 |
Explicații
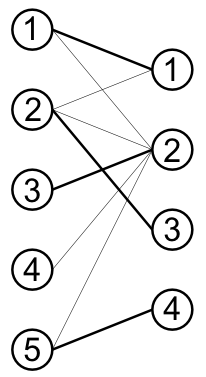
În graful din exemplu se vor cupla următoarele perechie de noduri: (1, 1), (2, 3), (3, 2), (5, 4).
Indicații de rezolvare
O scurtă lecție de teorie găsiți aici și în cartea Introducere in algoritmi, Thomas Cormen, editura Agora, Cluj-Napoca.
O soluție exponențială cu metoda backtracking poate fi găsită ușor.
O soluție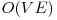 
cu algoritmul lui Edmonds Karp se găsește aici
O soluție ce folosește lanțuri altenante în complexitate 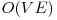se găsește aici. Menționez că acest algoritm se comportă foarte bine în practică.
Soluția de 100p se obține cu ajutorul algoritmului lui Hopcroft Karp de complexitate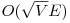 
și este o îmbunătățire a soluției precedente: la fiecare pas al iterației se găsește un număr maximal de lanțuri alternante care acceptă o augmentare de o unitate de flux. Această soluție se găsește aici
În grafuri bipartite, cuplajul maxim este egal cu acoperirea minimă cu noduri (minimum vertex cover). Din acest rezultat deducem că acoperirea minimă cu noduri (minimum vertex cover) și multimea maximă de puncte independente (maximum independent set) se pot rezolva în timp polinomial în grafuri bipartite.
Probleme suplimentare:
- Felinare
- Gandaci Java
- Paznici
- Taramul Nicaieri
- Knights, BalticOI 2001
- Beloved Sons
- Unstable Systems
- Black-White King Strikes Back
- Euler Circuit
- Gopher Strategy
- Royal Guards, CEOI 2002
- Muddy Fields
