Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | cuplaj1.in, cuplaj1.out | Sursă | |
| Autor | Autor necunoscut | Adăugată de |  Bogdan-Alexandru Stoica •fireatmyself |
| Timp execuţie pe test | 0.25 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Cuplaj Maxim
Se numeste graf bipartit un graf G ale carui noduri pot fi partitionate in doua multimi disjuncte A si B astfel incat oricare muchie uneste un nod din A si un nod din B. Cu alte cuvinte, nu exista doua nuduri i si j din aceeasi multime astfel incat sa existe muchie intre ele.
Fie G un graf bipartit. Numim cuplaj o submultime de muchii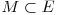 
(unde E este multimea muchiilor grafului) cu proprietatea ca ∀ i ∈ A exista cel mult o muchie in M incidenta in i. Spunem ca i este cuplat de cuplajul M daca exista o muchie in M incidenta in i. In caz contrar spunem ca i este necuplat. Numim cuplaj maxim o multime M de cardinal maxim, adica nu exista nicio alta multime M' cu |M'| > |M| (unde cu |M| am notat cardinalul multimii M).
Cerinta
Se da un graf bipartit G. Se cere sa se gaseasca valoarea cuplajului maxim.
Date de intrare
Pe prima linie a fisierului de intrare cuplaj1.in se afla N1, N2 si M. N1 reprezinta numarul de noduri ale multimii A, iar N2 numarul de noduri ale multii B. Pe urmatoarele M linii se afla cate doua numere a si b cu semnificatia ca intre nodurile a ∈ A si b ∈ B exista muchie.
Date de iesire
In fisierul de iesire cuplaj1.out se va scrie un singur numar, valoarea cuplajului maxim.
Restrictii
- 1 ≤ N1, N2 ≤ 2000
- 1 ≤ M ≤ 310 000
- nodurile multimii A sunt numerotate de la 1 la N1
- nodurile multimii B sunt numerotate de la 1 la N2
Exemplu
| cuplaj1.in | cuplaj1.out |
|---|---|
| 5 4 6 1 1 2 1 1 4 3 2 5 4 4 2 | 3 |
Indicatii
O metoda de rezolvare foloseste algoritmii de flux maxim:
Se construieste un graf G' pornind de la graful G la care mai adaugam doua noduri: o sursa si o destinatie. Toate nodurile multimii A se leaga de sursa respectiva si toate nodurile multimii B se leaga de destinatia respectiva. Se considera ca muchiile grafului G' au capacitatea 1. Valoarea cuplajului maxim in graful G este numeric egala cu valoarea fluxlui maxim din graful G'.
O solutie mai rapida si mult mai usor de implementat este cea care se bazeaza pe lanturi augmentative:
Pentru orice i din A definim Ri ca fiind nodul de care este acesta cuplat in B. De asemenea, pentru orice nod i din B, definim Li ca fiind nodul de care este acesta cuplat in A. Initial, vectorii au valoarile 0.
Pentru fiecare nod necuplat din A apelam functia recursiva pairup care va functiona astfel:
1. daca exista un vecin necuplat de-ai lui i (Ri = 0), il vom cupla cu acesta;
2. daca nu, incercam sa fortam cuplarea lui i (daca se poate) cu un vecin j deja cuplat; va trebui sa recuplam nodul de care era anterior legat j si vom apela recursiv functia pairup, de data aceasta pentru Lj.
La final, valoarea cuplajului maximal va fi egala cu numarul de noduri i cuplate, adica pentru care Ri > 0.
Pentru clarificarea algoritmului puteti consulata "":sursa.
Mai multe detalii despre cuplajul in graf bipartit, precum si probleme asemanatoare se pot gasi in acest aritcol.
