Fişierul intrare/ieşire:	copaci4.in, copaci4.out	Sursă	ONI 2012 - clasa a 9-a
Autor	Vlad Ionescu	Adăugată de	Simoiu Robert •SpiderMan
Timp execuţie pe test	0.2 sec	Limită de memorie	20480 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Copaci4

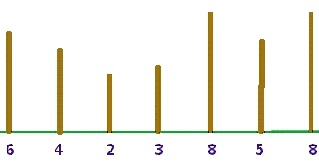
Se consideră n copaci de diferite înălţimi, aflaţi în linie dreaptă la distanţe egale, numerotaţi de la 1 la n. Pentru fiecare copac se cunoaşte înălţimea sa H_i. Cum şi copacii simt nevoia să socializeze, fiecare dintre ei are prieteni printre ceilalţi copaci. Prietenii oricărui copac i se pot afla atât la stânga, cât şi la dreapta sa. Relaţiile de prietenie sunt definite în felul următor: pentru fiecare copac i considerăm un şir d₁, d₂, ..., d_x reprezentând prietenii copacului i situaţi în dreapta sa şi un şir s₁, s₂ ... s_y reprezentând prietenii copacului i situaţi în stânga acestuia. Copacii din cele două şiruri corespunzătoare unui copac i formează împreună lista prietenilor acestuia. Şirurile corespunzătoare copacului i se definesc astfel:

1. • d₁ = i + 1 (dacă i = n, atunci copacul i nu are niciun prieten la dreapta sa, şirul rămânând vid);
   • pentru fiecare k ≥ 2, d_k este cel mai mic indice (1 ≤ d_k ≤ n) cu proprietatea că d_k > d_k-1 şi H_dk > H_dk-1. Dacă d_k nu există, atunci lista de prieteni la dreapta ai copacului i s-a încheiat şi construirea şirului se opreşte la acest pas.

1. • s₁ = i - 1 (daca i = 1, atunci copacul i nu are niciun prieten la stânga sa, sirul rămânând vid);
   • pentru fiecare k ≥ 2, s_k este cel mai mare indice (1 ≤ s_k ≤ n) cu proprietatea că s_k < s_k-1 şi H_sk > H _sk-1. Dacă s_k nu există, atunci lista de prieteni la stânga ai copacului i s-a încheiat şi construirea şirului se opreşte la acest pas.

Date de intrare

Fişierul de intrare copaci4.in ...

Date de ieşire

În fişierul de ieşire copaci4.out ...

Restricţii

• ... ≤ ... ≤ ...

Exemplu

Explicaţie

...

Cum se trimit solutii?