Fişierul intrare/ieşire:	clici.in, clici.out	Sursă	ad-hoc
Autor	Tudor Muresan	Adăugată de	Ciprian Oprisa •cypry
Timp execuţie pe test	0.25 sec	Limită de memorie	16384 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Clici disjuncte total interconectate prin lanțuri

Fie un graf neorientat 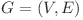format din clici disjuncte total interconectate prin lanţuri. O clică este o mulţime de vârfuri 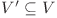cu proprietatea că între fiecare pereche de vârfuri din 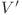există o muchie în 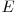. Un lanţ între nodurile 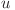şi 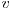este un drum elementar cu extremităţile 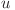şi 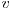. Toate celelalte noduri ale lanţului sunt distincte şi au gradul 2, adică au exact doi vecini. Pentru graful dat 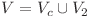, unde 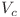este mulţimea nodurilor clicilor disjuncte (cu gradul mai mare ca 2), iar 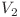este mulţimea nodurilor cu gradul 2. Clicile disjuncte sunt total interconectate prin lanţuri, dacă lanţurile au extremităţile în 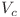şi celelalte noduri în 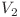, iar fiecare nod din 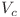este extremitatea unui singur lanţ.

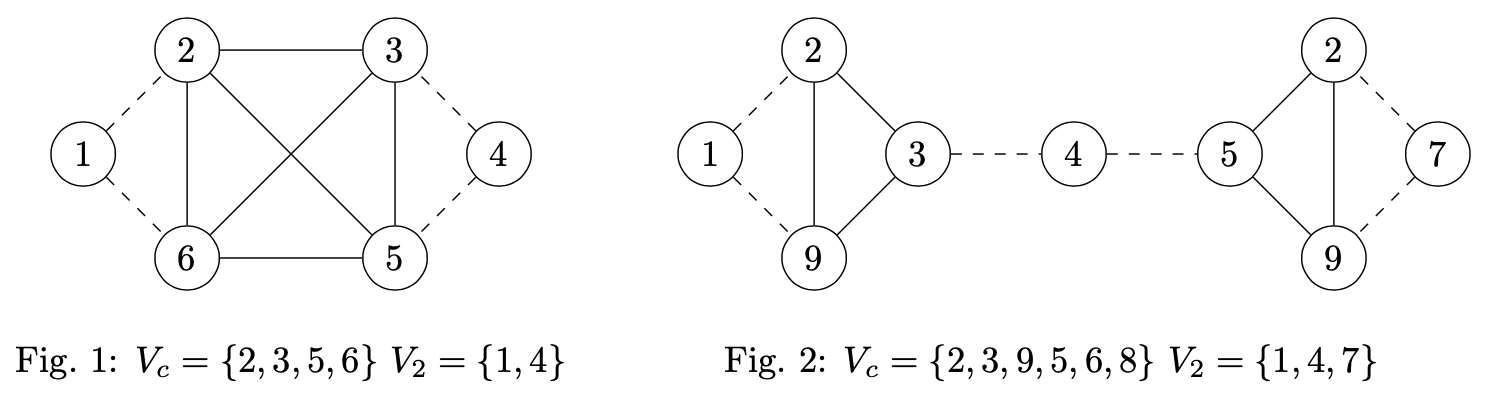
Fiind dat un graf 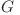format din clici disjuncte total interconectate prin lanţuri se cere să se găsească un ciclu Hamiltonian, adică un ciclu elementar, care trece prin fiecare vârf al grafului exact o singură dată. Graful din Fig. 1 are ciclul Hamiltonian 1, 2, 3, 4, 5, 6 iar cel din Fig. 2 nu are ciclu Hamiltonian.

Date de intrare

Fişierul de intrare clici.in conţine mai multe teste. Prima linie a testului conţine două numere întregi N şi M separate printr-un spaţiu, reprezentând numărul de noduri şi numărul de muchii ale grafului. Următoarea linie conţin 2M numere întregi separate de spaţiu, fiecare pereche de numere consecutive reprezentând o muchie a grafului (vârfurile sunt numere de la 1 la N). Este garantat că fiecare muchie apare o singură dată şi că extremităţile fiecărei muchii sunt distincte. Fişierul se termină cu numărul 0.

Date de ieşire

În fişierul de ieşire clici.out se tipăreşte pentru fiecare test o singură linie care începe cu numărul exemplului de test, urmat de caracterul ':' şi de cuvântul 'nu' dacă graful nu conţine un ciclu Hamiltonian sau 'da' urmat de N noduri (numere separate prin spaţiu), care constituie ciclul Hamiltonian, dacă acesta există (trebuie să existe o muchie inclusiv între ultimul nod şi primul). Dacă există mai multe soluţii se acceptă oricare din ele.

Restricţii

• 3 ≤ N ≤ 1000
• 1 ≤ M ≤ 100000
• fişierul de intrare conţine cel mult 20 de teste

Exemplu

Cum se trimit solutii?