| Fişierul intrare/ieşire: | clepsidra.in, clepsidra.out | Sursă | ONI 2014, clasele 11-12 |
| Autor | Radu Stefan Voroneanu | Adăugată de | |
| Timp execuţie pe test | 0.25 sec | Limită de memorie | 36864 kbytes |
| Scorul tău | N/A | Dificultate |
Vezi solutiile trimise | Statistici
Clepsidra
Un graf conex cu N noduri şi M muchii poate fi privit ca o clepsidră cu centrul în nodul X, 1 ≤ X ≤ N, dacă putem împărţi toate nodurile, mai puţin nodul X, în două submulţimi nevide astfel încât orice drum de la un nod dintr-o mulţime la un nod din cealaltă mulţime trece prin nodul X. Voi trebuie să determinaţi numărul de moduri distincte în care putem privi graful ca o clepsidră pentru fiecare din cele N noduri alese drept centru, modulo 666013. Două moduri se consideră distincte dacă cele două submulţimi aferente sunt diferite. Ordinea submulţimilor într-un mod este relevantă, dar ordinea nodurilor în cadrul unei mulţimi nu este. Spre exemplu, soluţiile ({1,2,3}, {4,5}) şi ({4,5}, {1,2,3}) sunt distincte, dar soluţiile ({4,5}, {1,2,3}) şi ({4,5}, {1,3,2}) nu sunt distincte.
Date de intrare
Fişierul de intrare clepsidra.in conţine pe prima linie două numere naturale, N şi M, reprezentând numărul de noduri, respectiv numărul de muchii din graf. Pe următoarele M linii se vor afla câte două numere naturale separate prin câte un spaţiu, reprezentând câte o muchie.
Date de ieşire
În fişierul de ieşire clepsidra.out se vor afişa N linii. A i-a linie, 1 ≤ i ≤ N, va conţine numărul de moduri în care putem privi graful ca o clepsidră cu centrul în nodul i, modulo 666013.
Restricţii
- 2 ≤ N ≤ 200 002
- 1 ≤ M ≤ 250 002
- Pentru 40% din teste avem restricţiile 2 ≤ N ≤ 1002 şi 1 ≤ M ≤ 1502.
- Atentie! Graful este conex.
Exemplu
| clepsidra.in | clepsidra.out | Explicaţie |
|---|---|---|
| 6 7 4 3 1 3 5 4 4 1 3 2 1 5 5 6 | 0 0 2 0 2 0 | 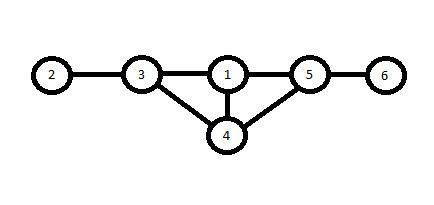
|


