Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | acces.in, acces.out | Sursă | ONI 2011 - clasa a 10-a |
| Autor | Dan Pracsiu | Adăugată de | |
| Timp execuţie pe test | 0.325 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Acces
Considerăm o matrice cu L linii (numerotate de sus în jos de la 1 la L) şi C coloane (numerotate de la stânga la dreapta de la 1 la C) care memorează doar valori 0 şi 1. Mai mult, valorile egale cu 1 sunt grupate în mai multe dreptunghiuri pline, care nu se învecinează nici pe linii, nici pe coloane, nici pe diagonale. În exemplul din fig. 1 matricea este corectă deoarece cele 4 dreptunghiuri de 1 nu se învecinează. În schimb în fig. 2 există 2 dreptunghiuri de 1 învecinate pe coloană şi două învecinate pe diagonală, deci matricea este incorectă.
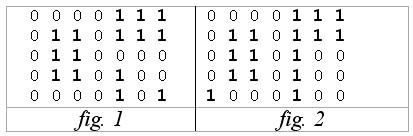
În această matrice se pot face deplasări doar pe direcţiile Vest şi Nord în elemente egale cu 0, deci din poziţia (i, j) se poate ajunge doar într-una dintre poziţiile (i, j-1) şi (i-1, j), marcate cu 0. În acest fel, pornind de la o anumită poziţie, prin deplasări succesive, pot fi accesate un anumit număr de elemente ale matricei egale cu 0. De exemplu, în fig. 1, din poziţia (2, 4) pot fi accesate 5 componente egale cu 0, iar din poziţia (5, 4) pot fi accesate 14 componente egale cu 0.
Trebuie să răspundeţi la Q întrebări, fiecare întrebare fiind de forma: “Câte din elementele egale cu zero ale matricei pot fi accesate din poziţia $(i, j)?$”
Cerinţă
Scrieţi un program care să determine, pentru fiecare întrebare, câte elemente egale cu 0 din matrice pot fi accesate din poziţia precizată în cadrul întrebării.
Date de intrare
Fişierul de intrare acces.in ...
Date de ieşire
În fişierul de ieşire acces.out ...
Restricţii
- ... ≤ ... ≤ ...
Exemplu
| acces.in | acces.out |
|---|---|
| This is some text written on multiple lines. | This is another text written on multiple lines. |
Explicaţie
...
