Sandokan
Observam ca elementul maxim din sir va ramane tot timpul in configuratia finala. Datorita acestul fapt, la fiecare pas putem alege elementul maxim impreuna cu alte K-1 elemente pe care le vom elimina. Deci daca configuratia finala contine P elemente, unul din cele P elemente este elementul maxim, iar restul de P-1 le putem alege in toate modurile posibile. Raspunsul la problema noastra este Combinari(N-1, P-1). Ca detaliu de implementare, puteam folosi recurenta C[n][k] = C[n-1][k-1]+C[n-1][k], obtinand complexitate O(N2) ca timp si memorie O(N) (avem nevoie doar de ultimele doua linii din matrice). O alta varianta ar fi fost sa plecam de la faptul ca 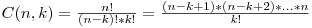 . Putem itera k de la 1 la P-1 si fiecare termen de forma n-k+i il vom imparti atat pe el cat si pe k la cmmdc(k, n-k+i). La sfarsit va trebui doar sa inmultim valorile care au ramas la numarator.
. Putem itera k de la 1 la P-1 si fiecare termen de forma n-k+i il vom imparti atat pe el cat si pe k la cmmdc(k, n-k+i). La sfarsit va trebui doar sa inmultim valorile care au ramas la numarator.
