Revizia anterioară Revizia următoare
Solutii preONI 2006 - Runda 1
(Categoria Competitii, autor(i) Echipa infoarena)
Runda 1 a concursului preONI 2006 s-a incheiat. Acest articol contine solutiile oficiale pentru toate probleme propuse spre rezolvare, cat si comentarii referitoare la concurs.
Fiecare grupa a avut spre rezolvare 3 probleme, fiecare fiind catalogata de catre comisie ca fiind usoara, medie sau grea. Batalia pentru calificarea la finala este abia la inceput!
Pentru mai multe detalii despre finala, cat si despre concursul preONI 2006 si sponsorii nostri va rugam sa consultati pagina preONI-2006.
Rezultatele finale sunt disponibile la:
Din pacate, punctajele la clasele a 9-a si a 10-a sunt sub asteptarile comisiei. Pentru discutii despre dificultate problemelor si despre concursul preONI 2006 in general va invitam sa intrati pe forum.
Inainte de a va prezenta solutiile va invitam sa rezolvati problemele propuse la acest concurs in Arhiva de probleme infoarena, si va asteptam in forta la runda a 2-a a concursului! (17 decembrie 2005)
Reuniune
(clasa a 9-a problema usoara)
Vom considera cazul simplificat cu 2 dreptunghiuri A si B, pentru care putem obtine formulele:
- Arie(A + B) = Arie(A) + Arie(B) - Arie(A x B)
- Perim(A + B) = Permi(A) + Perim(B) - Perim(A x B)
(A+B reprezinta reuniunea multimilor A si B, iar AxB intersectia.)
Cazul cu 3 dreptunghiuri A, B, C se rezolva similar. Cea mai simpla metoda este de a "vizualiza" formula facand un desen. Mai jos aveti un astfel de desen ajutator.
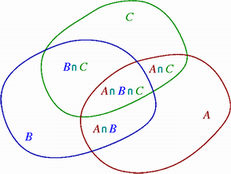
Asadar, obtinem formula:
- Arie(A+B+C) = Arie(A) + Arie(B) + Arie(C) - Arie(AxB) - Arie(BxC) - Arie(AxC) + Arie(AxBxC)
(pentru perimetru formula este asemanatoare)
Astfel rezolvarea este O(1), deoarece intersectia a 2 sau 3 dreptunghiuri poate fi calculata usor in timp constant. Mentionam ca formula de mai sus poate fi gasita si pe cale algebrica, si reprezinta un caz particular al principiului includerii si excluderii.
Patrate 2
(clasa a 9-a problema medie)
Mai intai sa completam matricea doar cu 1 si 5 astfel incat produsul elementelor de pe fiecare linie sau coloana sa fie 5. Observam ca pe fiecare linie si pe fiecare coloana se plaseaza exact un 5, restul matricii fiind completata cu 1. Este evident ca fiecare permutare a multimii (1, 2 * N) reprezinta de fapt o posibilitate de aranjare a numarului 5 in matrice, iar de aici deducem ca numarul de posibilitati de a completa matricea doar cu 1 si 5 este PN (adica N!). Cum putem folosi si -1 si -5, rezultatul final va fi 2N*N*N!
La implementare trebuie sa se efectueze operatii cu numere mari. De asemenea, se recomanda ca baza in care se lucreaza trebuie sa fie destul de mare pentru a se obtine eficienta dorita.
Invers (solutie oferita de Bogdan Tataroiu)
(clasa a 9-a problema grea, clasa a 10-a problema usoara)
Rezolvarea acestei probleme presupune parcurgerea numarului ce trebuie verificat (il vom nota cu v) din exterior spre interior. Notam cu s pozitia extremitatii stangi al numarului, iar cu d pozitia extremitatii drepte. Astfel numarul v este format prin adunarea unor numere de forma
- a1 a2 a3 ... an-2 an-1 an
- an an-1 an-2 ... a3 a2 a1
Asadar, prin adunarea cifrelor ai si an-1+1 se poate obtine un transport care va afecta cifrele anterioare. Deoarece sirul este parcurs de la extremitati spre interior s va fi egal cu i, iar d va fi egal cu n - i + 1, deci cifrele vs si vd sunt formate prin adunarea cifrelor ai si an-i+1.
In parcurgerea sirului de la extremitati catre interior cazul ideal este atunci cand vs este egal cu vd, caz in care cifra vs nici nu primeste si nici nu trimite transport la cifrele aflate pe pozitii anterioare.
Un alt caz este cel in care vs primeste transport prin adunarea cifrelor as+1 si ad-1 (vezi schema de mai sus pentru a intelege acest lucru). In acest caz vs este egal cu vd+1 si, pentru a tine cont de faptul ca pozitia s+1 a generat transport, adaugam la vs+1 valoarea 10.
Un al treilea caz este acela in care vs da transport pentru cifra vs-1 si nu primeste transport de la s+1, in acest caz vs fiind egal cu vd+10 (acel 10 fiind adaugat la pasul anterior). Deoarece atat vs cat si vd sunt obtinute prin adunarea cifrelor as si ad, iar vs da transport cifrelor anterioare, atunci si vd da transport cifrelor anterioare. Pentru a corecta acest lucru cifra vd-1 trebuie decrementata, avand grija la cazurile in care vd-1 este egal cu 0. De asemenea trebuie luat in calcul cazul in care vd este egal cu 9 si vs=19. Acest lucru este imposibil deoarece suma maxima a doua cifre este 18 si, evident, va trebui sa se afiseze raspunsul NU.
Al patrulea si ultimul caz este acela in care vs da transport cifrei vs-1 si, in acelasi timp, primeste transport de la cifrele aflate pe pozitia s+1. In acest caz vs=vd+11 si trebuie executate atat operatiile pt cazul vs=vd+1, cat si cele pentru cazul vs=vd+10.
Daca diferenta vs-vd este diferita de 0, 1, 10 si 11 atunci numarul v nu poate fi obtinut prin adunarea unui numar a cu inversul sau.
Algoritmul se repeta pana cand s devine egal cu d, caz in care cifra vs=vd trebuie sa fie para pentru ca numarul v sa indeplineasca conditia din enunt sau pana cand d=s+1, caz in care trebuie ca vs=vd sau vs=vd+11 pentru ca numarul v sa aiba proprietatea ceruta.
Se mai considera cazul cand a1=0, iar v1=1,obtinut printr-un transport : se aduna 10 la v2 si se considera numarul incepand de la pozitia a doua, caruia i se verifica validitatea. Atentie la cazuri particulare!
Pentru a intelege mai bine algoritmul general vom analiza urmatorul exemplu: 7 2 2 3 2 6.
Observand ca 7=6+1 tragem concluzia ca prima cifra va trebui sa primeasca transport, deci vom analiza 12 2 3 2. Observam din nou ca 12=2+10 ceea ce inseamna ca 12 trebuie sa trimita transport in fata, deci si 2 din coada va fi de fapt 12. Vom lua inapoi transportul de la 3, deci vom analiza in continuare 2 2. Acestea fiind egale nu se primeste si nu se da transport. Deoarce nu sa dat peste nici o contradictie raspunsul va fi DA.
Complexitatea acestui algoritm este O(nr) pe test, unde nr este numarul de cifre al numarului v.
Dreptunghi
(clasa a 10-a problema medie)
Un dreptunghi care apare in grila de puncte laticiale e marginit de doua drepte verticale la stanga si la dreapta, si de doua drepte orizontale in sus si in jos. Acum, daca vrem pentru patru drepte fixate sa stim cate dreptunghiuri marginesc ele, ne putem uita la urmatorul desen.
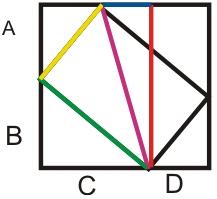
Daca dreptunghiul determinat de cele patru drepte are laturile H si W atunci un dreptunghi inscris va imparti laturile lui in bucatile A, B si C, D. Acum folosind teorema lui Pitagora avem ca:
- A2 + D2 = Galben2
- B2 + C2 = Verde2
- Galben2 + Verde2 = Roz2
- (A + B)2 = Rosu2
- 2 = Albastru2
- Rosu2 + Albastru2 = Roz2
De aici avem ca (A + B)2 + (C - D)2 = A2 + B2 + C2 + D2, astfel obtinem AB = CD, dar B = H - A, iar D = W - C deci avem ca C2 - WC + A(H - A) = 0. Daca il fixam pe A atunci trebuie sa rezolvam o ecuatie de gradul doi in necunoscuta C, solutia trebuie sa fie intreaga intre 0 si W.
Astfel in O(H) vom sti numarul de dreptunghiuri inscrise intr-un dreptunghi de dimensiuni H * W. Acest dreptunghi poate fi pus in (N - H + 1) * (M - H + 1) locatii pe o grila de dimensiune N * M. Deci solutia are complexitate O(N*M2), pentru fiecare dreptunghi de dimensiuni 1 ≤ H ≤ N$ si 1 ≤ W ≤ M calculandu-se numarul de dreptunghiuri inscrise.
O rezolvare de complexitate O(N2*M2) in care se cautau solutiile ecuatiei printr-un for ar fi luat 60 de puncte. Rezolvarea directa folosind ecuatia de gradul doi ia in jur de 80 de puncte. Algoritmul poate fi optimizat la factorii constanti, de exemplu avem nevoie de functia radical care este cam inceata, precalculand-o obtinem o accelerare a vitezei, alta idee ar fi ca numarul de solutii cu A ≤ H/2 este egal cu numarul de solutii cu A ≥ H - H/2 si a treia idee de optimizare este ca numarul de dreptunghiuri inscrise intr-un dreptunghi de dimensiuni H, W este acelasi cu numarul de dreptunghiuri inscrise intr-un dreptunghi de dimensiuni W, H.
Zebughil
(clasa a 10 problema grea, clasele 11-12 problema medie)
Se poate aborda o rezolvare bazata pe parcurgerea numerelor de la 1 la 3n-1 in ordine. Pastram matricea best in care retinem numarul minim de camioane in care pot fi transportate blocurile date de bitii de 1 din i. Completarea acestei matrici se face in O(3n). Descompunerea in baza 3 va avea urmatoarea semnificatie: 0 - blocul nu e in multimea curenta, 1 - blocul se afla in ultimul camion sau 2 - blocul se afla intr-un camion anterior in care nu se mai poate aduaga.
Aceasta idee aduce 90 de puncte daca este implementata corect. O alta solutie se poate obtine daca avem in vedere faptul ca avem limita superioara 500 pentru capacitatea unui camion putem face o rezolvare ce foloseste principiul programrii dinamice. Vom folosi o matrice besti,j care retine numarul minim de camioane astfel incat sa putem transporta blocurile identificate de bitii de 1 din reprezentarea in baza 2 a lui i, iar ultimul camion sa fie plin pana la capacitatea j. Aceasta solutie ar fi obtinut 70 de puncte.
Deoarece fie folosim maxim n camioane fie nu avem solutie putem incerca construirea unei matrici besti,j cu semnificatia cat mai este liber in ultimul camion ca sa avem transportati bitii de 1 din i si sa folosim maxim j camioane. Completarea acestei matrici se face in O(2n*n2), aducand 100 de puncte.
Analizand mai departe observam ca nu este nevoie sa retinem pentru o configuratie decat solutia folosind numar minim de camioane deoarece daca am folosi mai multe putem pur si simplu sa incepem unul nou acuma care va avea capacitate G. Astfel complexitatea de memorie se reduce la O(2n) iar cea de timp la O(2n*n)
O alta abordare interesanta a problemei dar care nu ducea la obtinerea unui punctaj maxim este generarea permutarilor prin backtracking si testarea greedy a solutiei. Parcurgem permutarea si cand avem nevoie de un camion nou il deschidem. Aceasta ar avea o complexitatea O(n!*n). Putem insa retine pe parcurs costul pana in acel moment si la sfarsit sa nu trebuiasca sa mai parcurgem din nou. Pentru generarea permutarilor se poate retine o lista cu elementele care nu au fost inca puse in permutare lista in care un element se va adauga si se va scoate in O(1). Aceasta tehnica se numeste dancing links si duce la o complexitate totala de O(n!)
O abordare neortodoxa ar fi fost generarea aleatoare a permutarilor, astfel pornim de la o permutare initiala si luam doua elemente din permutare in mod aleator pe care le interschimbam, daca solutia obtinuta e mai buna sau cel putin egala cu solutia initiala (valoarea unei solutii o vedem folosind un algoritm greedy care baga in ordine elementele in camioane) atunci pastram solutia curenta, iar daca nu interschimbam elementele la loc. O asemenea tehnica de optimizare a solutiei ar fi dus la un punctaj de aproximativ 60 de puncte.
Distante
(clasele 11-12, problema usoara)
Foarte multi concurenti au incercat sa rezolve aceasta problema folosind algoritmul Dijkstra cu heap-uri sau cu arbori de intervale. Aceasta solutie ar fi obtinut de la 70 pana la 100 de puncte (in cazul in care se optimiza algoritmul). O alta metoda de a obtine 100 de puncte ar fi fost folosirea algoritmul Bellman Ford cu coada (vezi OJI 2004, problema Lanterna).
Solutia oficiala (care este de fapt si cea mai simpla si cea mai usor de implementat) are complexitate O(N+M) ca timp si O(N) ca memorie. Ea poate fi dedusa din modul de functionare a algoritmilor Dijkstra sau Bellman Ford. Asadar, conditile suficiente si necesare ca distantele minime date sa fie corecte sunt:
- DS = 0
- Dx + cost(x, y) ≥ Dy pentru orice muchie (x, y)
- exista pentru fiecare y (diferit de S) un x astfel incat Dx + cost(x, y) = Dy
Studiati modul in care functioneaza Dijkstra sau Bellman Ford si veti vedea ca logica acestor conditii devine evidenta. Verificarea acestor conditii se poate face in complexitatea mentionata mai sus.
Balans
(clasele 11-12, problema grea)
Problema a fost gandita sa rasplateasca pe "fanii infoarena" si anume pe aceea care au rezolvat corect problemele Secventa 1, Secventa 2, Secventa 3. Pentru a trata circularitatea matricii o vom extinde intr-o matrice 2N*2M, lipind matrii initiale o copie la dreapta, sub ea, si la dreapta-jos.
Rezolvarea acum se va baza pe cautarea binara a balansului maxim (idee folosita si la rezolvarea problemei Secventa 3). Fie acesta X, trebuie sa verificam daca exista o submatrice cu balans cel putin X, adica:
- Suma / Numar ≥ X
- Suma ≥ X*Numar
- Suma - X*Numar ≥ 0
Folosind cele scrise mai sus, putem observa ca, daca fiecare element nr din matricea intiala este inlocuit cu nr-X, atunci problema se reduce la a determina o submatrice din matricea modificata in care suma elementelor este ≥ 0. Aceasta problema se poate rezolva determinand submatricea de suma maxima din matricea modificata, verificand apoi daca este ≥ 0.
Asadar, problema s-a redus la a determina o submatrice de cel putin R linii si C coloane de suma maxima dintr-o matrice. Intai vom fixa 2 linii la distanta cel putin R si cel mult N, si vom calcula sumele pe coloane intre cele doua linii (acest lucru se poate face in O(M) precalculand anumite sume la inceput). Pe vectorul de sume pe coloane obtinut va trebui sa rezolvam acum problema "secventei de suma maxima de lungime intre C si M" (necesara si la rezolvarea problemei Secventa 3). Fie A vectorul pe care vrem sa rezolvam acesta problema, si Si = A1+A2+...+Ai. Pentru fiecare i va trebui sa gasim un j astfel incat:
- S[i] - S[j] = maxim
- i-M ≤ j ≤ i-C
Acest lucru se poate face in O(M) per total folosind structura "deque" , prezentata pe scurt si in articolul cu solutii de la preONI 2005, runda 3. Lasam detalierea modului in care se va folosi aceasta structura in rezolvare ca exercitiu pentru cititor. Astfel, problema poate fi rezolva in complexitatea O(N2*M*lg MAX) unde MAX este valoarea maxima din matricea. Mentionam ca pentru o solutie relativ rapida si care sa evite erori de precizie se recomanda lucrul cu numere intregi (inmultind totul cu 1000).
