Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2009-11-01 15:03:58.
Revizia anterioară Revizia următoare

Programare dinamica

(Categoria Tehnici de programare, autor Catalin Tiseanu)

Plan de atac (probleme-candidat):

1. http://www.main.edu.pl/user.phtml?op=showtask&task=wie&con=PA2009&lang=en
Reducerea complexitatii, transformarea problemei intr-una de construire a unui arbore binar.

2. http://code.google.com/codejam/contest/dashboard?c=32001#s=p0&a=3

3. http://code.google.com/codejam/contest/dashboard?c=32001#s=p3&a=3

4. http://code.google.com/codejam/contest/dashboard?c=32015#s=p1&a=1

5. http://code.google.com/codejam/contest/dashboard?c=32010#s=p3&a=3

Sugestii Silviu

poate ca nu trebuie sa spunem tot despre programare dinamica intr-un singur articol; spre exemplu putem facem doua articole: PD basic si PD advanced
cred ca era si ceva prin Cartea lui Francu' despre programare dinamica; ar merge incorporat (eventual in pd_basic).

Introducere

Programarea dinamică este o metodă utilă pentru a rezolva probleme care pot fi obţinute prin compunerea a mai multor bucăţi, a căror soluţie poate fi apoi determinată optim. Se bazează în principal pe proprietatea unei probleme de a putea fi rezolvată optim dacă se cunosc soluţii optime la sub-problemele ei.
De menţionat că 'programare' nu se referă aici la scrierea de cod într-un limbaj de programare, ci la 'programare matematica', care constă în optimizarea unei funcţii prin alegerea de valori dintr-o mulţime anume.

Scopul acestui articol nu este să ofere o introducere in programare dinamică (pentru aceasta poate fi consultat excelentul tutorial de pe TopCoder Dynamic Programming : From novice to advanced). În schimb, acest articol îşi propune să ofere nişte 'smenuri' mai avansate de rezolvare a problemelor cu programare dinamică.

Programare dinamică cu reducerea loop-ului interior

Să considerăm următoarea problema:

Problema 1: Drilling

Se da un şir de N numere naturale (a₁, a₂, ..., a_N). Se ştie că un prefix al acestui şir (adică o subsecvenţă de la începutul şirului, posibil nulă) este defect. Toate elementele din acel prefix (şi doar din acel prefix) sunt defecte. Se ştie de asemenea că se poate testa orice poziţie i în timp a_i pentru a afla dacă este defectă. Să se determine timpul minim în cazul cel mai defavorabil pentru aflarea lungimii maxime a prefixului şirului care este defect.

Exemplu:

Pentru secvenţa de numere (8 24 12 6), răspunsul ar fi 42. Astfel, se testează mai întâi poziţia 2. Dacă nu este defectă, mai rămâne de testat poziţia 1. Altfel, în cel mai rău caz mai trebuie testate poziţiile 3 şi 4, aducând timpul total la 24 + 12 + 6 = 42.

Rezolvare:

O să începem prin a da altă îmbrăcăminte problemei. Astfel, să ne imaginăm că am construi un arbore binar de căutare pe şirul dat, având drept chei poziţiile din şir, şi drept valori auxiliare valorile poziţiilor respective din şir (un nod cu cheia i va avea valoarea auxiliara a_i.
Acum, există mulţi arbori binari de căutare posibile pentru şirul iniţial. Totuşi, să presupunem că am construit unul, pe care îl considerăm de acum ca fixat. Atunci, strategia noastra de testare a elementelor din şir se va desfăşura conforma arborelui. Astfel, testăm mai întâi în poziţia din rădăcină. Dacă poziţia respectivă este defectă, ne ducem în fiul drept. Altfel, mergem in fiul stâng. În ambele cazuri se reia procedeul. Căutarea se termină cand nu mai putem merge într-un fiu.

Să observăm că dacă considerăm costul unui drum în arbore de la rădăcină la o frunză ca suma valorilor auxiliare din drumul (unic) respectiv, atunci se observă că costul strategiei bazate pe acest arbore este chiar costul maxim al unui drum ! De acum încolo, vom defini costul unui arbore ca costul maxim al unui drum din el. Să exemplificăm pe şirul din exemplu:

BAGA POZA

Se observă că costul maxim al unui drum este 42, minim posibil, exact ca răspunsul din exemplu.
Deci, am redus problema la construirea unui arbore binar de căutare, care are costul minim.

Acum devine clară o primă soluţie folosind programarea dinamică. Astfel, să presupunem că notăm cu $opt[ i ][ j ]$ costul minim al unui arbore construit pe cheile din [i, j] (prin asta notăm (i, i + 1, ..., j). Fie $r[ i ][ j ]$ poziţia rădăcinii arborelui cu costul minim. În cazul existenţei mai multor rădăcini posibile, se alege cea mai din stânga. 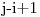Cum am putea construi arborele de cost minim pe cheile [i,j] ştiind răspunsul pentru instanţele mai mici (subsecvenţele de lungime mai mică ca $j-i+1$ pe [i,j])? 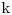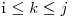(!) Simplu, arborele de cost minim pe [i,j] se obţine alegând drept rădăcină în mod optim o poziţie $k$ , cu $i \le k \le j$ , la care se pune ca fiul stâng arborele optim pentru [i, k-1], şi ca fiu drept arborele optim pentru [k+1, j]. Relaţia de recurenţă devine:

$$opt[ i ][ j ]$ = \displaystyle\min_{i \le k \le j} \{a_{k} + \max( opt[i][k-1], opt[k+1][j] )\}$
$$r[ i ][ j ]$ = \displaystyle\arg \min_{i \le k \le j}\{a_{k} + \max (opt[i][k-1], opt[k+1][j] )\}$

Avem $opt[i][j] = 0$ , pentru j < i.
Cazurile de bază sunt $opt[i][i] = a_i$ si $r[i][i] = i$ .

Se observă că răspunsul problemei se află în $opt[1][N]$ .
Astfel, am obţinut o soluţie în timp O(N^3).

Aici trebuie remarcată asemănarea acestei probleme cu cea a determinării arborelui de căutare optim, atunci cand se dau probabilităţile relative de căutare a cheilor. Această problemă se numeşte 'Optimal Binary Search Tree' în literatura de specialitate şi poate fi găsită şi în Introduction to Algorithms. În aceasta problemă, se poate aplica o proprietate specială, numită convexitate, pentru a reduce complexitatea la O(N^2). Această proprietate reprezintă un concept avansat, care nu se poate aplica în cazul problemei noastre, şi nu va fi discutat în continuare.
[]